SmoothlyBrokenPowerLawa 1 D

class astropy.modeling.powerlaws.SmoothlyBrokenPowerLaw1D(amplitude=1, x_break=1, alpha_1=- 2, alpha_2=2, delta=1, **kwargs)

ベースクラス: astropy.modeling.core.Fittable1DModel

1次元の安定したべき乗則モデルを打破します

パラメータ

amplitude浮いている.

切断点におけるモデル振幅。

x_break浮いている.

断れ。

alpha_1浮いている.

べき乗指数は x << x_break それがそうです。

alpha_2浮いている.

べき乗指数は x >> x_break それがそうです。

delta浮いている.

平滑度パラメータ。

参考

BrokenPowerLaw1D

注意事項

Model formula (with \(A\) for amplitude, \(x_b\) for x_break, \(\alpha_1\) for alpha_1, \(\alpha_2\) for alpha_2 and \(\Delta\) for delta):

\[F(X)=A\Left(\frac{x}{x_b}\Right)^-\Alpha_1} \左\{0} \crc{1}{2} \左[ 1+\Left(\frac{x}{x_b}\Right)^{1/\Delta} \右] \右\}^{(\Alpha_1-\Alpha_2)\Delta}\]

傾きの変化は2つの値の間で起こる \(x_1\) そして \(x_2\) そのために：

\[\log_{10}\frac{x_2}{x_b}=\log_{10}\frac{x_b}{x_1} \SIM\Delta\]

AT値 \(x \lesssim x_1\) そして \(x \gtrsim x_2\) このモデルは指数付き単純べき乗モデルに近似している。 \(\alpha_1\) そして \(\alpha_2\) それぞれです。この2つのべき乗は値に滑らかに結合されている。 \(x_1 < x < x_2\) したがって、そのために \(\Delta\) パラメータは勾配変更の“滑らかさ”を設定する.

♪the delta パラメータは1 e−3より大きい値に制限される(対応する \(x_2 / x_1 \gtrsim 1.002\) )オーバーフローエラーを回避します。

♪the amplitude このモデルは通常正数を表すために用いられるため，パラメータは正の値に制限される.

実例.

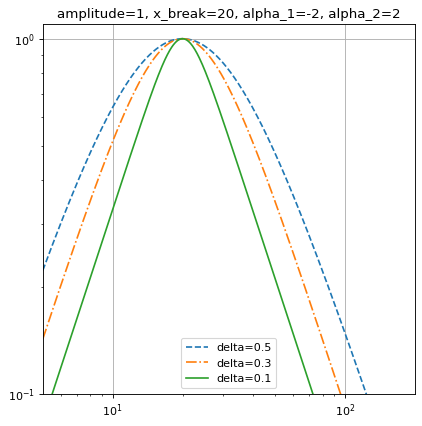
import numpy as np
import matplotlib.pyplot as plt
from astropy.modeling import models

x = np.logspace(0.7, 2.3, 500)
f = models.SmoothlyBrokenPowerLaw1D(amplitude=1, x_break=20,
                                    alpha_1=-2, alpha_2=2)

plt.figure()
plt.title("amplitude=1, x_break=20, alpha_1=-2, alpha_2=2")

f.delta = 0.5
plt.loglog(x, f(x), '--', label='delta=0.5')

f.delta = 0.3
plt.loglog(x, f(x), '-.', label='delta=0.3')

f.delta = 0.1
plt.loglog(x, f(x), label='delta=0.1')

plt.axis([x.min(), x.max(), 0.1, 1.1])
plt.legend(loc='lower center')
plt.grid(True)
plt.show()

(png, svg, pdf)

属性要約

alpha_1 \
alpha_2 \
amplitude \
delta \
input_units \	この属性は、Evaluateメソッドがどの単位または単位セットを必要とするかを示し、入力を単位にマッピングする(または)ことを返すために使用される None 任意の単位が受け入れられていれば).
param_names \	このタイプモデルのパラメータ名を記述する.
x_break \

方法要約

evaluate \(X，振幅，x_Break，Alpha1，...)	1次元滑らかで欠けたべき乗モデル関数
fit_deriv \(X，振幅，x_Break，Alpha1，...)	1次元の滑らかで欠けたべき乗パラメータ導関数

属性文書

alpha_1 = Parameter('alpha_1', value=-2.0)

alpha_2 = Parameter('alpha_2', value=2.0)

amplitude = Parameter('amplitude', value=1.0, bounds=(0, None))

delta = Parameter('delta', value=1.0, bounds=(0.001, None))

input_units

param_names = ('amplitude', 'x_break', 'alpha_1', 'alpha_2', 'delta')

このタイプモデルのパラメータ名を記述する.

このタプル内のパラメータの順序は、特定のタイプのモデルを初期化する際に入力されるべき順序と同じである。いくつかのタイプのモデル(例えば、多項式モデル)は、次数のようなモデルのいくつかの他の属性に依存する異なる数のパラメータを有する。

モデルクラスを定義する際には，その属性の値は Parameter クラス主体で定義された属性.

x_break = Parameter('x_break', value=1.0)

方法文書

static evaluate(x, amplitude, x_break, alpha_1, alpha_2, delta)

1次元滑らかで欠けたべき乗モデル関数

static fit_deriv(x, amplitude, x_break, alpha_1, alpha_2, delta)

1次元の滑らかで欠けたべき乗パラメータ導関数