Ripley K関数推定器¶
天文環境では、空間相関関数は、別のオブジェクトの所与の距離内でオブジェクト(例えば、銀河)が発見される確率を推定するために使用されている 1.
RipleyのK関数は、このような空間点プロセスの相関を特徴付けるための推定器である。 2, 3, 4, 5, 6. より正確には、所与のフィールドにおけるオブジェクト間の相関を記述する。♪the RipleysKEstimator クラスは、この関数のいくつかの推定器を実装し、これは、いくつかのエッジ効果補正方法を提供する。
基本的用法¶
The actual implementation of Ripley's K function estimators lie in the method
evaluate, which take the following arguments: data, radii, and
optionally, mode.
♪the data 引数は1つの二次元配列であり,研究領域中の1組の観測点(イベント)を表す.♪the radii パラメータは、推定器の値を求める距離のセットに対応する。♪the mode パラメータは以下の言語集合の値を用いる {{none, translation, ohser, var-width, ripley}} 各キーワードは、エッジ効果によって補正を実行する異なる方法を表す。これらの方法の詳細については、API文書および参照を参照されたい。
実例. RipleysKEstimator 呼び出し可能なオブジェクトとしても使えます(これは呼び出しに相当します evaluate 方法)。
例を引く¶
RipleyのK関数推定器を用いて astropy 統計サブパック:
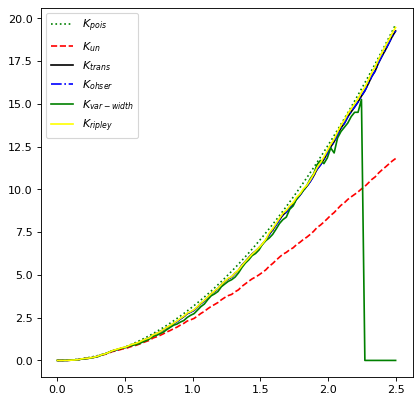
import numpy as np
from matplotlib import pyplot as plt
from astropy.stats import RipleysKEstimator
z = np.random.uniform(low=5, high=10, size=(100, 2))
Kest = RipleysKEstimator(area=25, x_max=10, y_max=10, x_min=5, y_min=5)
r = np.linspace(0, 2.5, 100)
plt.plot(r, Kest.poisson(r), color='green', ls=':', label=r'$K_{pois}$')
plt.plot(r, Kest(data=z, radii=r, mode='none'), color='red', ls='--',
label=r'$K_{un}$')
plt.plot(r, Kest(data=z, radii=r, mode='translation'), color='black',
label=r'$K_{trans}$')
plt.plot(r, Kest(data=z, radii=r, mode='ohser'), color='blue', ls='-.',
label=r'$K_{ohser}$')
plt.plot(r, Kest(data=z, radii=r, mode='var-width'), color='green',
label=r'$K_{var-width}$')
plt.plot(r, Kest(data=z, radii=r, mode='ripley'), color='yellow',
label=r'$K_{ripley}$')
plt.legend()
参考文献¶
- 1
ピアース、P.J.E. 宇宙の大スケール構造 それがそうです。<https://ui.adsab.atherard.edu/abs/1980 lsssu.book.P>
- 2
レイプリルB.D. The second-order analysis of stationary point processes それがそうです。確率雑誌を適用する。1976年13:255-266。
- 3
空間記述的統計 それがそうです。<https://en.wikipedia.org/wiki/Spatial_Descriptive_Statistics>
- 4
ノースカロライナ州クレシ 空間データ統計 寄稿:ワイリーニューヨーク
- 5
トップページ--定期刊行物の主な分類--定期刊行物の詳細紹介--定期刊行物の題録とダイジェスト フラクタルランダム形状点場 トップページ--定期刊行物の主な分類--定期刊行物の詳細紹介--定期刊行物の題録とダイジェスト--定期刊行物の詳細なダイジェスト内容
- 6
相関関数 それがそうです。<https://en.wikipedia.org/wiki/関連関数_(天文学)>