discretize_model

astropy.convolution.discretize_model(model, x_range, y_range=None, mode='center', factor=10)

メッシュ上の解析モデル関数を計算するための関数。

これまで，この関数は画素座標しか扱えなかった.

パラメータ

型番 ： FittableModel あるいは呼び寄せることができる。FittableModelまたはCallableである.

離散化された解析モデル関数が必要である.呼び出し可能なオブジェクトは FittableModel 伝達することができます custom_model そして評価を行う.

x_rangeタプル.

モデルのX範囲を評価する.上限と下限の差は整数でなければならず，出力配列サイズをうまく定義することができる.

y_rangeメタグループ、オプション

モデルのY範囲を評価する.上限と下限の差は整数でなければならず，出力配列サイズをうまく定義することができる.2次元モデルのみに必要である.

mode文字列、オプション

以下のモデルの1つ：

• 'center' (約束を)破る

  箱の中心の値をとることでモデルを離散化する.

• 'linear_interp'

  モデルは，ボックス角点における値間で線形補間を行うことで離散化される.2 Dモデルの場合、補間は双線形である。

• 'oversample'

  過サンプリンググリッド上の平均値をとることでモデルを離散化する.

• 'integrate'

  倉位にモデルを統合することでモデルを離散化する. scipy.integrate.quad それがそうです。とても遅いです。

factor浮動型または整型

オーバーサンプリング係数。デフォルト値=10です。

返品

配列. ： numpy.arraynumpy.array

モデル値配列

注意事項

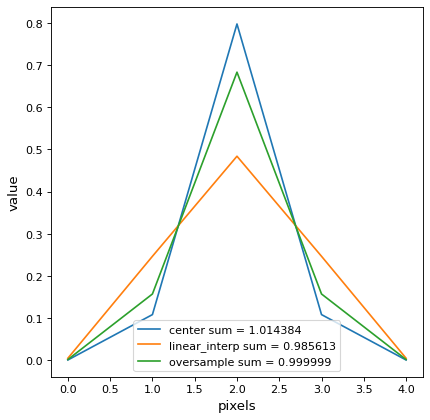
♪the oversample モードは、サブピクセル尺度上に積分を保存することを可能にする。以下に正規化ガウス1 Dの一例を示す。

import matplotlib.pyplot as plt
import numpy as np
from astropy.modeling.models import Gaussian1D
from astropy.convolution.utils import discretize_model
gauss_1D = Gaussian1D(1 / (0.5 * np.sqrt(2 * np.pi)), 0, 0.5)
y_center = discretize_model(gauss_1D, (-2, 3), mode='center')
y_corner = discretize_model(gauss_1D, (-2, 3), mode='linear_interp')
y_oversample = discretize_model(gauss_1D, (-2, 3), mode='oversample')
plt.plot(y_center, label='center sum = {0:3f}'.format(y_center.sum()))
plt.plot(y_corner, label='linear_interp sum = {0:3f}'.format(y_corner.sum()))
plt.plot(y_oversample, label='oversample sum = {0:3f}'.format(y_oversample.sum()))
plt.xlabel('pixels')
plt.ylabel('value')
plt.legend()
plt.show()

(png, svg, pdf)