Astropy座標における処理速度¶
以下の場合は速度を使用する SkyCoord¶
速度を持つ座標オブジェクトの取得を開始する最適な方法は SkyCoord インターフェースです。
実例.¶
A SkyCoord 測定された半径方向速度を持つが自身の運動や距離を知らない恒星を表すには、以下のように作成することができる。
>>> from astropy.coordinates import SkyCoord
>>> import astropy.units as u
>>> sc = SkyCoord(1*u.deg, 2*u.deg, radial_velocity=20*u.km/u.s)
>>> sc
<SkyCoord (ICRS): (ra, dec) in deg
(1., 2.)
(radial_velocity) in km / s
(20.,)>
>>> sc.radial_velocity
<Quantity 20.0 km / s>
SkyCoord このようにして作成されたオブジェクトは、すべての同じ変換規則に従い、他のフレームに変換されるときにその速度を正確に更新する。例えば、銀河系座標における恒星の自己と、ICRSで測定された自己を決定するためには、以下の操作を行う。
>>> sc = SkyCoord(1*u.deg, 2*u.deg, pm_ra_cosdec=.2*u.mas/u.yr, pm_dec=.1*u.mas/u.yr)
>>> sc.galactic
<SkyCoord (Galactic): (l, b) in deg
( 99.63785528, -58.70969293)
(pm_l_cosb, pm_b) in mas / yr
( 0.22240398, 0.02316181)>
有効操作と速度サポート制限の詳細については、ご参照ください astropy.coordinates (特に current accuracy limitations )については、より低いレベルのフレームオブジェクトにおける速度サポートに関する以下のより詳細な説明を参照されたい。これら全てのルールは SkyCoord オブジェクトは,Frameクラスの速度機能に直接構築されているため,ここでは詳細に説明する.
速度データを用いたフレームワークオブジェクトの作成¶
座標フレームは、記憶および変換速度データ(位置座標データとともに)をサポートする。使用のように Representation クラスは特定の表現を抽象化して再表現(例えば,デカルトから球面)を許可し,速度データを利用する. Differential 同じことをするように分類されています(差異クラスに関するより多くの情報は、参照されたい 表現法の微分と導関数 )位置データと同様に、差分(速度)成分の名前は、特定の座標フレームに依存する。
Most frames expect velocity data in the form of two proper motion components
and/or a radial velocity because the default differential for most frames is the
SphericalCosLatDifferential class. When supported, the
proper motion components all begin with pm_ and, by default, the
longitudinal component is expected to already include the cos(latitude)
term. For example, the proper motion components for the ICRS frame are
(pm_ra_cosdec, pm_dec).
実例.¶
自コンポーネント形式の速度データを使用してフレームオブジェクトを作成するには、以下の操作を実行してください。
>>> from astropy.coordinates import ICRS
>>> ICRS(ra=8.67*u.degree, dec=53.09*u.degree,
... pm_ra_cosdec=4.8*u.mas/u.yr, pm_dec=-15.16*u.mas/u.yr)
<ICRS Coordinate: (ra, dec) in deg
(8.67, 53.09)
(pm_ra_cosdec, pm_dec) in mas / yr
(4.8, -15.16)>
>>> ICRS(ra=8.67*u.degree, dec=53.09*u.degree,
... pm_ra_cosdec=4.8*u.mas/u.yr, pm_dec=-15.16*u.mas/u.yr,
... radial_velocity=23.42*u.km/u.s)
<ICRS Coordinate: (ra, dec) in deg
(8.67, 53.09)
(pm_ra_cosdec, pm_dec, radial_velocity) in (mas / yr, mas / yr, km / s)
(4.8, -15.16, 23.42)>
上の Galactic ボックスにおいて、名前追跡経度および緯度名:
>>> from astropy.coordinates import Galactic
>>> Galactic(l=11.23*u.degree, b=58.13*u.degree,
... pm_l_cosb=21.34*u.mas/u.yr, pm_b=-55.89*u.mas/u.yr)
<Galactic Coordinate: (l, b) in deg
(11.23, 58.13)
(pm_l_cosb, pm_b) in mas / yr
(21.34, -55.89)>
位置データと同様に速度データは Quantity 物体です。
フレームワークによって予想されるパラメータ名を制御するために、予期される差分クラスを変更することができる。デフォルトの場合、正しい運動コンポーネントは含まれなければなりません cos(latitude) しかしこれは指定することで SphericalDifferential クラス(デフォルトではありません SphericalCosLatDifferential ):
>>> from astropy.coordinates import SphericalDifferential
>>> Galactic(l=11.23*u.degree, b=58.13*u.degree,
... pm_l=21.34*u.mas/u.yr, pm_b=-55.89*u.mas/u.yr,
... differential_type=SphericalDifferential)
<Galactic Coordinate: (l, b) in deg
(11.23, 58.13)
(pm_l, pm_b) in mas / yr
(21.34, -55.89)>
これは,予想される表示クラスを指定することと並行して動作し,差分クラスが表示と互換性があればよい.例えば、デカルト座標中のすべての座標および速度成分を指定するには、以下の動作を実行してください。
>>> from astropy.coordinates import (CartesianRepresentation,
... CartesianDifferential)
>>> Galactic(u=103*u.pc, v=-11*u.pc, w=93.*u.pc,
... U=31*u.km/u.s, V=-10*u.km/u.s, W=75*u.km/u.s,
... representation_type=CartesianRepresentation,
... differential_type=CartesianDifferential)
<Galactic Coordinate: (u, v, w) in pc
(103., -11., 93.)
(U, V, W) in km / s
(31., -10., 75.)>
注意してください。 Galactic フレームは、デカルト位置および速度成分の特別な標準名を有する。他のフレームではこれらは x,y,z そして v_x,v_y,v_z **
>>> ICRS(x=103*u.pc, y=-11*u.pc, z=93.*u.pc,
... v_x=31*u.km/u.s, v_y=-10*u.km/u.s, v_z=75*u.km/u.s,
... representation_type=CartesianRepresentation,
... differential_type=CartesianDifferential)
<ICRS Coordinate: (x, y, z) in pc
(103., -11., 93.)
(v_x, v_y, v_z) in km / s
(31., -10., 75.)>
任意の表現形態の速度データを有する任意のフレームについては、一般的なフォーマットの下位速度データにより容易にアクセスすることができる速記もある。3 D速度データを有する任意のフレームオブジェクトについて、以下のコマンドを使用して3 Dデカルト速度にアクセスすることができる:
>>> icrs = ICRS(ra=8.67*u.degree, dec=53.09*u.degree,
... distance=171*u.pc,
... pm_ra_cosdec=4.8*u.mas/u.yr, pm_dec=-15.16*u.mas/u.yr,
... radial_velocity=23.42*u.km/u.s)
>>> icrs.velocity
<CartesianDifferential (d_x, d_y, d_z) in km / s
( 23.03160789, 7.44794505, 11.34587732)>
1つの検索に利用できるショートカットもあります Quantity 2次元自然運動データを含み、半径方向(視線)速度を検索するためのオブジェクト:
>>> icrs.proper_motion
<Quantity [ 4.8 ,-15.16] mas / yr>
>>> icrs.radial_velocity
<Quantity 23.42 km / s>
既存フレームワークオブジェクトへの速度追加¶
既存のFrameオブジェクトがあるとき(または SkyCoord )と、同じ位置を有するが速度を増加させたオブジェクトが欲しい。概念的には,最も直接的な方法は,差異の対象と realize_frame それがそうです。
実例.¶
以下のコードフラグメントは、明示的に定義された場合を実装し、必要な速度はデカルト表現の形態で知られている。既存フレームに速度を追加するには、以下の操作を実行してください realize_frame **
>>> icrs = ICRS(1*u.deg, 2*u.deg, distance=3*u.kpc)
>>> icrs
<ICRS Coordinate: (ra, dec, distance) in (deg, deg, kpc)
(1., 2., 3.)>
>>> vel_to_add = CartesianDifferential(4*u.km/u.s, 5*u.km/u.s, 6*u.km/u.s)
>>> newdata = icrs.data.to_cartesian().with_differentials(vel_to_add)
>>> icrs.realize_frame(newdata)
<ICRS Coordinate: (ra, dec, distance) in (deg, deg, kpc)
(1., 2., 3.)
(pm_ra_cosdec, pm_dec, radial_velocity) in (mas / yr, mas / yr, km / s)
(0.34662023, 0.41161335, 4.29356031)>
全3 D座標が利用できなくても(例えば、未知のオブジェクトからの半径方向速度観測)であっても、同様の機構を使用して速度を追加することができる。しかし,明確な単位情報が不足しているため,やや異なる指定の違いが必要となる.
>>> from astropy.coordinates import RadialDifferential
>>> icrs_no_distance = ICRS(1*u.deg, 2*u.deg)
>>> icrs_no_distance
<ICRS Coordinate: (ra, dec) in deg
(1., 2.)>
>>> rv_to_add = RadialDifferential(500*u.km/u.s)
>>> data_with_rv = icrs_no_distance.data.with_differentials({'s':rv_to_add})
>>> icrs_no_distance.realize_frame(data_with_rv)
<ICRS Coordinate: (ra, dec) in deg
(1., 2.)
(radial_velocity) in km / s
(500.,)>
生成されたオブジェクトは、オブジェクトを作成する際に半径方向速度を指定したときに得られるオブジェクトと同じであることが分かる。
>>> ICRS(1*u.deg, 2*u.deg, radial_velocity=500*u.km/u.s)
<ICRS Coordinate: (ra, dec) in deg
(1., 2.)
(radial_velocity) in km / s
(500.,)>
速度変換フレームを使う¶
速度データを含む座標フレームインスタンスを異なるフレーム(位置および速度変換を含む場合がある)に変換する方法は、位置フレームインスタンスのみを変換する方法と全く同じである。
例を引く¶
速度データを含む座標枠を変換するには、以下の操作を実行してください。
>>> from astropy.coordinates import Galactic
>>> icrs = ICRS(ra=8.67*u.degree, dec=53.09*u.degree,
... pm_ra_cosdec=4.8*u.mas/u.yr, pm_dec=-15.16*u.mas/u.yr)
>>> icrs.transform_to(Galactic())
<Galactic Coordinate: (l, b) in deg
(120.38084191, -9.69872044)
(pm_l_cosb, pm_b) in mas / yr
(3.78957965, -15.44359693)>
しかしながら、速度成分がどのように変換されるかの詳細な情報は、開始フレームから所望のフレームへの必要な特定の変換セット(すなわち、フレーム変換パターンによって使用される経路)に依存する。もし変換チェーンのすべてのフレームが BaseAffineTransform サブクラス(すなわち、行列変換またはアフィン変換)であれば、これらの変換は、速度データに明示的に適用することができる。そうでなければ,位置変換を有限差分することで速度変換を数値的に計算する.この2つの方法のより詳細については,次の節を参照されたい.
アフィン変換.¶
Frame transformations that involve a rotation and/or an origin shift and/or
a velocity offset are implemented as affine transformations using the
BaseAffineTransform subclasses:
StaticMatrixTransform,
DynamicMatrixTransform, and
AffineTransform.
行列変換(例えば、回転など)のみ ICRS 至る Galactic )は、自身の動きに限定されたデータまたは全空間3 D速度で実行されてもよい。
実例.¶
行列変換のみを実行するには、以下の動作を実行してください。
>>> icrs = ICRS(ra=8.67*u.degree, dec=53.09*u.degree,
... pm_ra_cosdec=4.8*u.mas/u.yr, pm_dec=-15.16*u.mas/u.yr,
... radial_velocity=23.42*u.km/u.s)
>>> icrs.transform_to(Galactic())
<Galactic Coordinate: (l, b) in deg
(120.38084191, -9.69872044)
(pm_l_cosb, pm_b, radial_velocity) in (mas / yr, mas / yr, km / s)
(3.78957965, -15.44359693, 23.42)>
位置ベクトルと速度ベクトルに同じ回転行列を適用する.速度オフセットに関する任意の変換は、すべての3 D速度成分(一般に距離を指定する必要もある)、例えば、すべての3 D速度成分を必要とする。 ICRS 至る LSR **
>>> from astropy.coordinates import LSR
>>> icrs = ICRS(ra=8.67*u.degree, dec=53.09*u.degree,
... distance=117*u.pc,
... pm_ra_cosdec=4.8*u.mas/u.yr, pm_dec=-15.16*u.mas/u.yr,
... radial_velocity=23.42*u.km/u.s)
>>> icrs.transform_to(LSR())
<LSR Coordinate (v_bary=(11.1, 12.24, 7.25) km / s): (ra, dec, distance) in (deg, deg, pc)
(8.67, 53.09, 117.)
(pm_ra_cosdec, pm_dec, radial_velocity) in (mas / yr, mas / yr, km / s)
(-24.51315607, -2.67935501, 27.07339176)>
有限差分変換¶
あるフレーム変換はアフィン変換として表すことができない.例えばここから来たのは AltAz フレームは、本質的に非線形である大気分散補正を含むことができる。さらに、いくつかのフレームは、アフィン変換に変換することができても、関数としてより容易に実装される。これらのフレームについては、有限差分法を使用して速度を変換することができる。この方法の実装は、ユーザ定義のフレームワークを同じ方法で使用することができることに留意されたい(すなわち、定義によって FunctionTransformWithFiniteDifference タイプ)。
この有限差分手法は、実際には、変換の2つの独立した(ただし重要な)要素を組み合わせている。
改革開放以来,中国経済発展の新しい局面 方向.方向 開始フレームに存在している速度ベクトルの。すなわち、フレーム変換は、リダイレクト座標フレーム(例えば、回転)に関する場合があり、新しいフレームにおける速度ベクトルは、この点を考慮しなければならない。有限差分方法は、速度ベクトルに沿って開始フレームの位置を移動させ、目標フレームにおいてオフセットを計算することによってモデル化される。
フレームワーク運動による“誘導”速度 それ自体が それがそうです。例えば,太陽系重心を中心とした座標系から地球を中心とした座標系への移動には,地球の重心周りの運動による速度成分が完全に含まれている。これは、目標フレームにおける開始フレームの位置をわずかに異なる時間で計算し、これらの位置間の差異を計算することにより実現される。このステップは、特定のフレーム属性が誘導速度に関連する“時間”を表すと仮定することに依存することに留意されたい。これは一般的には
obtime有限差分変換関数を定義する際に設定可能なオプションであるにもかかわらず、フレーム属性。
例を引く¶
有限差分変換には有限差分アルゴリズムと機器精度による内的制約があることを認識することが重要である.この問題を説明するために,AltAzからGCR(すなわち地心)への変換が考えられる.GCRSフレームワークにおいて、地球上から観察される半径方向速度10キロ/秒、距離100 AUの物体の径方向速度を計算してみましょう。
import numpy as np
from matplotlib import pyplot as plt
from astropy import units as u
from astropy.time import Time
from astropy.coordinates import EarthLocation, AltAz, GCRS
time = Time('J2010') + np.linspace(-1,1,1000)*u.min
location = EarthLocation(lon=0*u.deg, lat=45*u.deg)
aa = AltAz(alt=[45]*1000*u.deg, az=90*u.deg, distance=100*u.au,
radial_velocity=[10]*1000*u.km/u.s,
location=location, obstime=time)
gcrs = aa.transform_to(GCRS(obstime=time))
plt.plot_date(time.plot_date, gcrs.radial_velocity.to(u.km/u.s))
plt.ylabel('RV [km/s]')
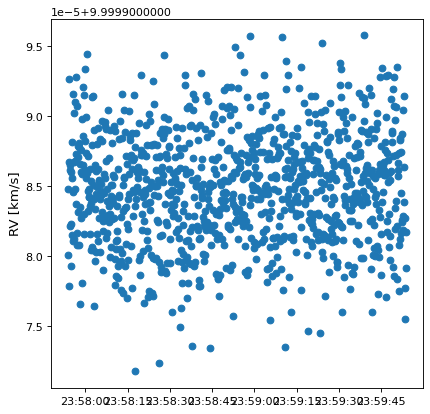
これは合理的に見える:半径方向速度は確かに10キロ/秒に非常に近いべきであり、フレームは速度オフセットに関連していないからである。
100について考えてみましょう 千パ秒 距離のように。この場合、2つのフレームにおける半径方向速度は実質的に同じであるべきであることが望ましい。
time = Time('J2010') + np.linspace(-1,1,1000)*u.min
location = EarthLocation(lon=0*u.deg, lat=45*u.deg)
aa = AltAz(alt=[45]*1000*u.deg, az=90*u.deg, distance=100*u.kpc,
radial_velocity=[10]*1000*u.km/u.s,
location=location, obstime=time)
gcrs = aa.transform_to(GCRS(obstime=time))
plt.plot_date(time.plot_date, gcrs.radial_velocity.to(u.km/u.s))
plt.ylabel('RV [km/s]')
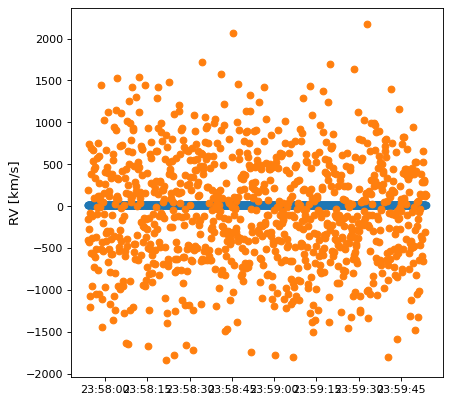
しかしこの結果はナンセンスであり,我々が期待している ̄10 km/sではなく-1000から1000 km/sの範囲である.ここで問題の根源は,機械精度が千分秒レベル距離での千段階差を計算するのに不十分であることである.したがって,直接の有限差分法はデフォルト値を用いたこのような用例には適用できない.
有限差分が発生する時間ステップサイズをカバーすることができる.例えば:
>>> from astropy.coordinates import frame_transform_graph, AltAz, CIRS
>>> trans = frame_transform_graph.get_transform(AltAz, CIRS).transforms[0]
>>> trans.finite_difference_dt = 1 * u.year
>>> gcrs = aa.transform_to(GCRS(obstime=time))
>>> trans.finite_difference_dt = 1 * u.second # return to default
上記の例では、ちょうど1つの変換ステップしかありません AltAz 至る GCRS それがそうです。一般に、2つのフレーム間に複数のステップがある場合があり、または単一のステップが内部で他の変換を実行することができる。コンテキストマネージャをご利用いただけます impose_finite_difference_dt() 書き換えたい変換図に対して finite_difference_dt 上の all 図上の有限差分変換::
>>> from astropy.coordinates import frame_transform_graph
>>> with frame_transform_graph.impose_finite_difference_dt(1 * u.year):
... gcrs = aa.transform_to(GCRS(obstime=time))
でも気をつけて not 以上のような場合に支援を提供し,この場合,速度に関する時間尺度は秒である.(特定の方向に対する地球の速度は1年で大きく変化した。)
Astropyの将来のバージョンは、結果が数値的に安定し、より実用的になり、これらの(珍しくない)使用例に使用することができるように、このアルゴリズムを改善するであろう。
半径方向速度補正¶
また,Astropyは計算重心や日心径方向速度補正をサポートしている.将来的には、上記のフレームワークを使用した高度な便利な機能である可能性があるが、現在の実装は、十分な正確性を確保するために独立している(参照 半径方向速度補正 そして radial_velocity_correction 詳細はAPI文書を参照されたい)。
例を引く¶
この例は,特定の時間にKeck天文台から既知のRAとDEC上のある天体を観察した場合,この修正をどのように計算するかを示している.3 m/秒程度の精度で十分であれば、計算された補正値を任意の観測された半径方向速度に加算して、最終的な重心半径方向速度を決定することができる。
>>> from astropy.time import Time
>>> from astropy.coordinates import SkyCoord, EarthLocation
>>> # keck = EarthLocation.of_site('Keck') # the easiest way... but requires internet
>>> keck = EarthLocation.from_geodetic(lat=19.8283*u.deg, lon=-155.4783*u.deg, height=4160*u.m)
>>> sc = SkyCoord(ra=4.88375*u.deg, dec=35.0436389*u.deg)
>>> barycorr = sc.radial_velocity_correction(obstime=Time('2016-6-4'), location=keck)
>>> barycorr.to(u.km/u.s)
<Quantity 20.077135 km / s>
>>> heliocorr = sc.radial_velocity_correction('heliocentric', obstime=Time('2016-6-4'), location=keck)
>>> heliocorr.to(u.km/u.s)
<Quantity 20.070039 km / s>
補正オプション(例えば、位置、観測時間など)を指定するためのいくつかの異なる方法があることに留意されたい。ご参照ください radial_velocity_correction 詳細は文書を参照されたい。
の精度 radial_velocity_correction¶
以下のように計算した補正値 radial_velocity_correction 光学近似を用いる \(v = zc\) (会いましょう) スペクトル(ドップラー)当量 詳細については参照)を参照されたい.補正は、約3メートル/秒まで正確な補正を提供するために、任意の観測された半径方向速度に追加することができます。より正確な補正が必要な場合には、いくつかの細かい点に注意しなければなりません。
まず,重心は重力が一定の固定点であるため,常に重心補正を用いるべきである。日心はこれらの条件を満たしていないため,日心の修正は低精度な作業にしか適用できない。そのため,速度向上のために日心学校は radial_velocity_correction 地球表面のポテンシャルによる引力の赤移動などの影響は含まれていない。これらの理由で中国の質心校正は radial_velocity_correction 常に高精度な作業に使用されなければならない。
Cm/秒レベルの半径方向速度補正に必要な他の注意事項は参照 Wright & Eastman (2014) それがそうです。最も重要なのは、厳密に言えば、重心修復は 掛け算. したがって、あなたはそれを以下のように適用すべきです。
どこへ行くのか. \(v_t\) 真の半径方向速度です \(v_m\) 半径方向の速度を測定しています \(v_b\) 戻った重心で補正されているかどうか radial_velocity_correction それがそうです。このように重心補正を適用できなければ,3 m/sオーダーの誤差を招く。
中の質心修正 radial_velocity_correction is consistent with the IDL implementation 無限距離の光源に対して,Wright&Eastmann(2014)紙の強度は10 mm/sである.シャピロ遅延は含まれておらず,その論文の式28における光進行時間補正も含まれていない。1 cm/秒以上の精度が必要でない限り、無視する用語は重要ではありません。この精度が確かに必要な場合は、参照されてください。 Wright & Eastmann (2014) それがそうです。