天文座標系 (astropy.coordinates )¶
序言:序言¶
♪the coordinates ソフトウェアパッケージは、様々な天体/空間座標およびその速度成分を表すクラスと、通常の座標系間を統一的に変換するためのツールとを提供する。
スタート¶
最初に使う最良の方法は coordinates 使用です。 SkyCoord 級友たち。 SkyCoord オブジェクトは、指定された単位および座標フレームを有する位置(およびオプション速度)を入力することによってインスタンス化される。空の位置は通常 Quantity オブジェクトは,文字列名を用いてフレームを指定する.
例を引く¶
作成するには SkyCoord 対象はICRS(右揚角)を表す [RA] 赤緯、赤緯 [Dec] )空の位置::
>>> from astropy import units as u
>>> from astropy.coordinates import SkyCoord
>>> c = SkyCoord(ra=10.625*u.degree, dec=41.2*u.degree, frame='icrs')
の初期値設定項 SkyCoord 非常に柔軟であり、様々な便利なフォーマットで提供される入力をサポートする。以下の座標を初期化する方法は、上記の方法と同等である。
>>> c = SkyCoord(10.625, 41.2, frame='icrs', unit='deg')
>>> c = SkyCoord('00h42m30s', '+41d12m00s', frame='icrs')
>>> c = SkyCoord('00h42.5m', '+41d12m')
>>> c = SkyCoord('00 42 30 +41 12 00', unit=(u.hourangle, u.deg))
>>> c = SkyCoord('00:42.5 +41:12', unit=(u.hourangle, u.deg))
>>> c
<SkyCoord (ICRS): (ra, dec) in deg
(10.625, 41.2)>
上の例は、座標オブジェクトを作成する際に従うべきいくつかのルールを示している。
座標値は命名されていない位置パラメータとして提供することもでき,以下のキーワードパラメータで提供することも可能である.
raそしてdecあるいは、あるいはlそしてb(フレームに依存します)。座標.座標
frameキーワードはオプションですなぜならデフォルトではICRSそれがそうです。すべてのコンポーネントに角度単位を指定しなければならない,メソッドは入力である.
Quantityオブジェクト(例えば、10.5*u.degree)を値に含めることによって(例えば、'+41d12m00s')、または通過unitキーワード。
SkyCoord そして他のすべての coordinates オブジェクトは配列座標もサポートする.これらの座標の動作形態は、一意の座標と同じであるが、単一のオブジェクトに複数の座標を格納する。同じ動作を多くの異なる座標(例えば、ディレクトリから)に適用しようとする場合、これはリストよりも良い選択である。 SkyCoord 相手はそうなるからです much 操作をそれぞれに適用するよりも SkyCoord 1つは for 循環する。下の階のように ndarray データを含む例は SkyCoord 対象に対してスライス,整形などの操作を行うことができる. numpy バージョン1.17以降は、以下の機能と組み合わせて使用することができます numpy.moveaxis など、形に影響を与えます
.. doctest-requires:: numpy>=1.17
>>> import numpy as np
>>> c = SkyCoord(ra=[10, 11, 12, 13]*u.degree, dec=[41, -5, 42, 0]*u.degree)
>>> c
<SkyCoord (ICRS): (ra, dec) in deg
[(10., 41.), (11., -5.), (12., 42.), (13., 0.)]>
>>> c[1]
<SkyCoord (ICRS): (ra, dec) in deg
(11., -5.)>
>>> c.reshape(2, 2)
<SkyCoord (ICRS): (ra, dec) in deg
[[(10., 41.), (11., -5.)],
[(12., 42.), (13., 0.)]]>
>>> np.roll(c, 1)
<SkyCoord (ICRS): (ra, dec) in deg
[(13., 0.), (10., 41.), (11., -5.), (12., 42.)]>
訪問を調整する.¶
座標オブジェクトを持つと、完全な座標の文字列表現形式を得るために、座標の構成要素(例えば、RA、DEC)にアクセスすることができる。
コンポーネント値は、座標フレーム(例えば、ICRS、Galaxyなど)に依存する名前属性(通常は小文字)を使用してアクセスされる。デフォルトのICRSに対して,座標コンポーネント名は ra そして dec **
>>> c = SkyCoord(ra=10.68458*u.degree, dec=41.26917*u.degree)
>>> c.ra
<Longitude 10.68458 deg>
>>> c.ra.hour
0.7123053333333335
>>> c.ra.hms
hms_tuple(h=0.0, m=42.0, s=44.299200000000525)
>>> c.dec
<Latitude 41.26917 deg>
>>> c.dec.degree
41.26917
>>> c.dec.radian
0.7202828960652683
属性は座標を文字列に変換する. to_string() 方法:
>>> c = SkyCoord(ra=10.68458*u.degree, dec=41.26917*u.degree)
>>> c.to_string('decimal')
'10.6846 41.2692'
>>> c.to_string('dms')
'10d41m04.488s 41d16m09.012s'
>>> c.to_string('hmsdms')
'00h42m44.2992s +41d16m09.012s'
詳細についてはご参照ください 使用角度 それがそうです。
転化する.¶
新しい座標フレームに変換する便利な方法の1つは,適切に命名された属性にアクセスすることである.
例を引く¶
手に入れるには Galactic フレームワーク使用::
>>> c_icrs = SkyCoord(ra=10.68458*u.degree, dec=41.26917*u.degree, frame='icrs')
>>> c_icrs.galactic
<SkyCoord (Galactic): (l, b) in deg
(121.17424181, -21.57288557)>
より多くの制御を得るためには transform_to 方法では、この方法は、Frame名、Frameクラス、またはFrameインスタンスを受け入れる:
>>> c_fk5 = c_icrs.transform_to('fk5') # c_icrs.fk5 does the same thing
>>> c_fk5
<SkyCoord (FK5: equinox=J2000.000): (ra, dec) in deg
(10.68459154, 41.26917146)>
>>> from astropy.coordinates import FK5
>>> c_fk5.transform_to(FK5(equinox='J1975')) # precess to a different equinox
<SkyCoord (FK5: equinox=J1975.000): (ra, dec) in deg
(10.34209135, 41.13232112)>
この形の transform_to 天体座標を AltAz 座標、使用許可 SkyCoord 計画観測のツールとしていますこの点のより完全な例については,参照されたい 天体の高度·方位角の測定とマッピング それがそうです。
いくつかの座標フレームは AltAz 他のフレームに変換するか、または他のフレームから変換する際には、地球回転情報(UT 1−UTCオフセットおよび/または極シフト)が必要とされる。これらの地球自転値は,必要に応じて国際地球自転·参考システム(IERS)サービスから自動的にダウンロードされる。参照してください IERSデータアクセス (astropy.utils.iers ) この過程の詳細については、参照のこと。
表示法¶
これまで,我々はすべての例で球面座標表現を用いてきたが,これは内蔵フレームのデフォルト設定である.一般に、座標を初期化または使用するためには、異なる表現(例えば、デカルト表現またはシリンドリカル表現)を使用することが便利である。これは設定することで representation_type どのようなものでも SkyCoord オブジェクトまたは下位フレーム座標オブジェクト.
例を引く¶
デカルトやシリンドリカルなどの異なる表現を使用して座標を初期化または使用するには、以下の動作を実行してください。
>>> c = SkyCoord(x=1, y=2, z=3, unit='kpc', representation_type='cartesian')
>>> c
<SkyCoord (ICRS): (x, y, z) in kpc
(1., 2., 3.)>
>>> c.x, c.y, c.z
(<Quantity 1. kpc>, <Quantity 2. kpc>, <Quantity 3. kpc>)
>>> c.representation_type = 'cylindrical'
>>> c
<SkyCoord (ICRS): (rho, phi, z) in (kpc, deg, kpc)
(2.23606798, 63.43494882, 3.)>
すべての詳細については、ご参照ください 表示法 それがそうです。
距離¶
SkyCoord また、各フレームカテゴリは、フレームの原点からの距離を指定することもサポートされる。原点は特定の座標系に依存する;例えば,地球を中心に太陽系の重心を中心とすることができる,などである。
実例.¶
2つの角度および1つの距離は、3 D空間内の唯一の点を指定し、これは、座標をデカルト表現に変換することも可能である。
>>> c = SkyCoord(ra=10.68458*u.degree, dec=41.26917*u.degree, distance=770*u.kpc)
>>> c.cartesian.x
<Quantity 568.71286542 kpc>
>>> c.cartesian.y
<Quantity 107.3008974 kpc>
>>> c.cartesian.z
<Quantity 507.88994292 kpc>
距離が割り当てられている場合には SkyCoord 便利な方法は3 D情報を利用できるので、より強力だ。例えば、空間内の2点間の物理的な3次元間隔を計算するためには、以下の操作を実行してください。
>>> c1 = SkyCoord(ra=10*u.degree, dec=9*u.degree, distance=10*u.pc, frame='icrs')
>>> c2 = SkyCoord(ra=11*u.degree, dec=10*u.degree, distance=11.5*u.pc, frame='icrs')
>>> c1.separation_3d(c2)
<Distance 1.52286024 pc>
便利な方法¶
SkyCoord 例えば、2つの座標間の空中(すなわち、角度)および3 D分離の計算をサポートするなど、多くの便利な方法が定義される。
実例.¶
2つの座標間の空中と3次元分離を計算するには、以下の操作を実行してください。
>>> c1 = SkyCoord(ra=10*u.degree, dec=9*u.degree, frame='icrs')
>>> c2 = SkyCoord(ra=11*u.degree, dec=10*u.degree, frame='fk5')
>>> c1.separation(c2) # Differing frames handled correctly
<Angle 1.40453359 deg>
または交差マッチングディレクトリ座標(詳細は参照) カタログにマッチする ):
>>> target_c = SkyCoord(ra=10*u.degree, dec=9*u.degree, frame='icrs')
>>> # read in coordinates from a catalog...
>>> catalog_c = ...
>>> idx, sep, _ = target_c.match_to_catalog_sky(catalog_c)
♪the astropy.coordinates sub-package also provides a quick way to get coordinates for named objects, assuming you have an active internet connection. The from_name method of SkyCoord uses Sesame 特定の命名対象の座標を検索する.
特定の命名対象の座標を検索するには、以下の操作を実行してください。
>>> SkyCoord.from_name("PSR J1012+5307")
<SkyCoord (ICRS): (ra, dec) in deg
(153.1393271, 53.117343)>
場合によっては、オブジェクトのディレクトリ名に座標が埋め込まれる。このようなオブジェクト名については, from_name 名前から座標を解析することができます(所与の場合 parse=True 選択します。低速接続の場合、これは、同じオブジェクト名に対するゴマ照会よりもはるかに速い可能性がある。しかし、このようにして抽出された座標は、データベース座標と数分角秒異なる可能性があるため、このオプションは、座標が亜角秒精度を必要としない場合にのみ使用されることに留意されたい。
>>> SkyCoord.from_name("CRTS SSS100805 J194428-420209", parse=True)
<SkyCoord (ICRS): (ra, dec) in deg
(296.11666667, -42.03583333)>
地球上のサイト(主に天文台)では astropy.coordinates 迅速な取得を提供しています EarthLocation - of_site 方法:
>>> from astropy.coordinates import EarthLocation
>>> apo = EarthLocation.of_site('Apache Point Observatory')
>>> apo
<EarthLocation (-1463969.30185172, -5166673.34223433, 3434985.71204565) m>
利用可能なサイト名リストを表示するには、ご利用ください astropy.coordinates.EarthLocation.get_site_names() それがそうです。
任意の地球アドレス(例えば、観測ステーションではない)については、ご利用ください of_address 種類の方法。関数に伝達されるどのアドレスも、Google地図を使用して緯度および経度を検索し、任意にGoogle地図に問い合わせて位置の高さを取得してもよい。Googleマップと同様に、完全に指定された住所、位置名、都市名などにも適用可能です。
>>> EarthLocation.of_address('1002 Holy Grail Court, St. Louis, MO')
<EarthLocation (-26726.98216371, -4997009.8604809, 3950271.16507911) m>
>>> EarthLocation.of_address('1002 Holy Grail Court, St. Louis, MO',
... get_height=True)
<EarthLocation (-26727.6272786, -4997130.47437768, 3950367.15622108) m>
>>> EarthLocation.of_address('Danbury, CT')
<EarthLocation ( 1364606.64511651, -4593292.9428273, 4195415.93695139) m>
注釈
from_name, of_site, and of_address are for convenience, and hence are by design relatively low precision. If you need more precise coordinates for an object you should find the appropriate reference and input the coordinates manually, or use more specialized functionality like that in the astroquery あるいは…。 astroplan 付属小包です。
これらの方法は,インターネット上からデータを検索して天球や地球座標を決定することに注意されたい.オンラインデータは更新される可能性がありますので、スクリプトが長期的に再現可能であることを保証する必要がある場合は、ご参照ください 遠隔資源へのアクセス方法の使用ヒント/アドバイス 一節です。
半径方向速度観測値を計算する重心修正(サポートの高度でもある)のように、この機能を組み合わせてより複雑なタスクを実行することができる。 SkyCoord 方法-参照 半径方向速度補正 ):
>>> from astropy.time import Time
>>> obstime = Time('2017-2-14')
>>> target = SkyCoord.from_name('M31')
>>> keck = EarthLocation.of_site('Keck')
>>> target.radial_velocity_correction(obstime=obstime, location=keck).to('km/s')
<Quantity -22.359784554780255 km / s>
速度(自分と半径方向の速度)¶
位置座標を除いて coordinates ストレージと変換速度をサポートします。これらはより低いレベルの coordinate frame classes (バージョン3.0の新機能) SkyCoord 対象::
>>> sc = SkyCoord(1*u.deg, 2*u.deg, radial_velocity=20*u.km/u.s)
>>> sc
<SkyCoord (ICRS): (ra, dec) in deg
(1., 2.)
(radial_velocity) in km / s
(20.,)>
速度サポート(および制限)の詳細については、参照 Astropy座標における処理速度 ペイジ。
概要 astropy.coordinates 概念¶
注釈
♪the coordinates package from v0.4 onward builds from previous versions of the package, and more detailed information and justification of the design is available in APE (Astropy Proposal for Enhancement) 5 それがそうです。
ここで、私たちはパッケージと関連フレームワークの概要を提供する。この背景情報は使用に必要なものではない coordinates 特に使用しています SkyCoord 高度なクラスですが、より高度な使い方に役立ちます。特にあなた自身のフレームワーク、変換、または表現形式を作成します。もう1つの有用な背景情報は 重要な定義 なぜなら彼らは coordinates それがそうです。
coordinates オブジェクトに基づく三層システム構築:表示,フレームワーク,高度クラス.表示クラスは、デカルト座標または球極座標のような3次元データ点を格納する特別な方法である。フレームは、FK 5またはICRSのような特定の参照フレームであり、それらは、異なる表現形態でそのデータを格納することができるが、互いに明確に定義された変換を有する。これらの変換は astropy.coordinates.frame_transform_graph また、ユーザは、新たな変換を作成することができる。最後に高度な授業( SkyCoord )Frameクラスを使用するが、これらのオブジェクトによりアクセスしやすいインターフェースと、様々な便利な方法およびより多くの文字列解析機能とを提供する。
これらの概念を分離してより容易に拡張できる機能 coordinates それがそうです。これは、表現、フレームワーク、変換を個別に定義または拡張することを可能にし、依然として保持している。 SkyCoord 級友たち。
例えば:
見 天体の高度·方位角の測定とマッピング 使用について coordinates 観測動作のための機能.
Vbl.使用 astropy.coordinates¶
以下に示す個々のページには、ソフトウェアパッケージの使用に関するより詳細な情報が提供されている。
また、このパケット機能のもう1つのリソースは astropy.coordinates.tests.test_api_ape5 書類をテストする。これは,このパッケージの主要な機能の大部分を示しているため,本文書の有用な補完である.Astropyソースコードのコピーをダウンロードするか、IPythonセッションに以下を入力することで見ることができます。
In [1]: from astropy.coordinates.tests import test_api_ape5
In [2]: test_api_ape5??
性能提示¶
もしあなたが使っているのは SkyCoord 多くの異なる座標について、単一の座標を作成すれば SkyCoord 単独で作成するのではなく、座標配列を使用します。 SkyCoord 各個別座標のオブジェクト:
>>> coord = SkyCoord(ra_array, dec_array, unit='deg')
さらに循環トラバースは SkyCoord 物体はゆっくりできる。座標を異なるフレームに変換する必要がある場合、単一の変換 SkyCoord 数値配列を使うのではなく SkyCoord それぞれを改造しました
最後に、より高度なユーザーには、放送を使用して変換できることに注意してください SkyCoord ベクトル属性を持つフレームにオブジェクトを追加する.
例を引く¶
放送を利用して転換を実現する SkyCoord ベクトル属性を持つフレームにオブジェクトを追加する:
>>> from astropy.coordinates import SkyCoord, EarthLocation
>>> from astropy import coordinates as coord
>>> from astropy.coordinates.tests.utils import randomly_sample_sphere
>>> from astropy.time import Time
>>> from astropy import units as u
>>> import numpy as np
>>> # 1000 random locations on the sky
>>> ra, dec, _ = randomly_sample_sphere(1000)
>>> coos = SkyCoord(ra, dec)
>>> # 300 times over the space of 10 hours
>>> times = Time.now() + np.linspace(-5, 5, 300)*u.hour
>>> # note the use of broadcasting so that 300 times are broadcast against 1000 positions
>>> lapalma = EarthLocation.from_geocentric(5327448.9957829, -1718665.73869569, 3051566.90295403, unit='m')
>>> aa_frame = coord.AltAz(obstime=times[:, np.newaxis], location=lapalma)
>>> # calculate alt-az of each object at each time.
>>> aa_coos = coos.transform_to(aa_frame)
アレイの性能を向上させる obstime¶
観察者に依存する座標フレーム間の変換時に最も高価な動作(例えば、 AltAz )と空に固定されたフレーム(例えば ICRS )は、地球の方位と位置を計算するものである。
もし SkyCoord 事例は大量の密集した分布に変換されます obstime 各点の地球方位パラメータを計算するのではなく補間法を用いることにより,これらの計算速度を100倍に向上させることができ,微角秒精度を維持したままである。
座標変換に天文測定値を補間するには、使用してください。
>>> from astropy.coordinates import SkyCoord, EarthLocation, AltAz
>>> from astropy.coordinates.erfa_astrom import erfa_astrom, ErfaAstromInterpolator
>>> from astropy.time import Time
>>> from time import perf_counter
>>> import numpy as np
>>> import astropy.units as u
>>> # array with 10000 obstimes
>>> obstime = Time('2010-01-01T20:00') + np.linspace(0, 6, 10000) * u.hour
>>> location = location = EarthLocation(lon=-17.89 * u.deg, lat=28.76 * u.deg, height=2200 * u.m)
>>> frame = AltAz(obstime=obstime, location=location)
>>> crab = SkyCoord(ra='05h34m31.94s', dec='22d00m52.2s')
>>> # transform with default transformation and print duration
>>> t0 = perf_counter()
>>> crab_altaz = crab.transform_to(frame)
>>> print(f'Transformation took {perf_counter() - t0:.2f} s')
Transformation took 1.77 s
>>> # transform with interpolating astrometric values
>>> t0 = perf_counter()
>>> with erfa_astrom.set(ErfaAstromInterpolator(300 * u.s)):
... crab_altaz_interpolated = crab.transform_to(frame)
>>> print(f'Transformation took {perf_counter() - t0:.2f} s')
Transformation took 0.03 s
>>> err = crab_altaz.separation(crab_altaz_interpolated)
>>> print(f'Mean error of interpolation: {err.to(u.microarcsecond).mean():.4f}')
Mean error of interpolation: 0.0... uarcsec
>>> # To set erfa_astrom for a whole session, use it without context manager:
>>> erfa_astrom.set(ErfaAstromInterpolator(300 * u.s))
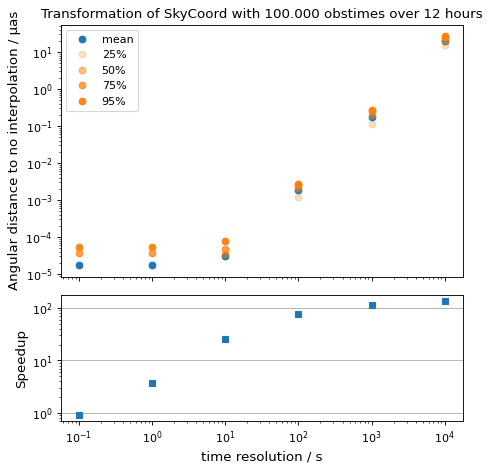
ここでは適切なものを選ぶことを考えています time_resolution それがそうです。1つの空の座標を複数回観察して ICRS 至る AltAz 異なる値計算精度と実行時間である. time_resolution 非補間のデフォルトメソッドと比較する.
from time import perf_counter
import numpy as np
import matplotlib.pyplot as plt
from astropy.coordinates.erfa_astrom import erfa_astrom, ErfaAstromInterpolator
from astropy.coordinates import SkyCoord, EarthLocation, AltAz
from astropy.time import Time
import astropy.units as u
np.random.seed(1337)
# 100_000 times randomly distributed over 12 hours
t = Time('2020-01-01T20:00:00') + np.random.uniform(0, 1, 10_000) * u.hour
location = location = EarthLocation(
lon=-17.89 * u.deg, lat=28.76 * u.deg, height=2200 * u.m
)
# A celestial object in ICRS
crab = SkyCoord.from_name("Crab Nebula")
# target horizontal coordinate frame
altaz = AltAz(obstime=t, location=location)
# the reference transform using no interpolation
t0 = perf_counter()
no_interp = crab.transform_to(altaz)
reference = perf_counter() - t0
print(f'No Interpolation took {reference:.4f} s')
# now the interpolating approach for different time resolutions
resolutions = 10.0**np.arange(-1, 5) * u.s
times = []
seps = []
for resolution in resolutions:
with erfa_astrom.set(ErfaAstromInterpolator(resolution)):
t0 = perf_counter()
interp = crab.transform_to(altaz)
duration = perf_counter() - t0
print(
f'Interpolation with {resolution.value: 9.1f} {str(resolution.unit)}'
f' resolution took {duration:.4f} s'
f' ({reference / duration:5.1f}x faster) '
)
seps.append(no_interp.separation(interp))
times.append(duration)
seps = u.Quantity(seps)
fig = plt.figure()
ax1, ax2 = fig.subplots(2, 1, gridspec_kw={'height_ratios': [2, 1]}, sharex=True)
ax1.plot(
resolutions.to_value(u.s),
seps.mean(axis=1).to_value(u.microarcsecond),
'o', label='mean',
)
for p in [25, 50, 75, 95]:
ax1.plot(
resolutions.to_value(u.s),
np.percentile(seps.to_value(u.microarcsecond), p, axis=1),
'o', label=f'{p}%', color='C1', alpha=p / 100,
)
ax1.set_title('Transformation of SkyCoord with 100.000 obstimes over 12 hours')
ax1.legend()
ax1.set_xscale('log')
ax1.set_yscale('log')
ax1.set_ylabel('Angular distance to no interpolation / µas')
ax2.plot(resolutions.to_value(u.s), reference / np.array(times), 's')
ax2.set_yscale('log')
ax2.set_ylabel('Speedup')
ax2.set_xlabel('time resolution / s')
ax2.yaxis.grid()
fig.tight_layout()
別項参照¶
ここで実装される座標系の細かい点を理解するために特に有用ないくつかの参照資料は、以下のことを含む。
- USNO Circular 179
ICRS/IERS/CIRSをめぐるIAU 2000/2003作業および精密座標系作業における関連問題に関する有用なガイドライン。
- Standards Of Fundamental Astronomy
IAUで定義されたアルゴリズムの最終的な実現.“地球態度ソファーツール”ファイルは、IAUの最新基準を詳細に知るために特に価値がある。
- IERS Conventions (2010)
詳細な参考資料は、ITRS、IAU 2000天文座標フレーム及び現代座標約束の他の関連詳細をカバーしている。
- Meeus J.“天文アルゴリズム”
これは座標に関する一連の問題や概念の詳細を記述した価値のある文章である。
- Revisiting Spacetrack Report #3
衛星軌道の簡略化広義摂動(SGP)を検討し,真赤道平均赤道(TEME)座標系を記述した。
内蔵フレーム類¶
Asterpy.cocoates.Builtin_Framesパッケージ¶
次の図は、すべての内蔵座標系、それらの別名(属性パターンアクセスを使用して他の座標をそれらに変換するために有用である)、およびそれらの間の所定の変換を示す。ユーザは、これらのシステム間で新しい変換を定義することによって、これらの変換のいずれかを自由にカバーすることができるが、所定の変換は、典型的な用法を満たすのに十分であるはずである。
図中の辺の色(すなわち、2フレーム間の変換)は、変換タイプによって設定され、図のブロックは、変換クラス名の色へのマッピングを定義する。
-
AffineTransform: ➝
-
FunctionTransform: ➝
-
FunctionTransformWithFiniteDifference: ➝
-
StaticMatrixTransform: ➝
-
DynamicMatrixTransform: ➝
クラス¶
|
ICRSシステムにおける座標またはフレーム. |
|
FK 5システムにおける座標またはフレーム。 |
|
FK 4システムにおける座標またはフレーム. |
|
FK 4システムでは座標またはフレームであるが,収差のE項は除去されている. |
|
銀河座標系における座標やフレームです |
|
銀河系の座標やフレームです |
このような制御は |
|
|
超銀河座標(Lahavらを参照)2000、<https://ui.adsab.atherard.edu/abs/2000 MNRAS.312..166 L>、およびその中の参考文献)。 |
高さ−方位角系ではWS 84に対するスフェロイドの座標やフレーム(水平座標)である。 |
|
|
地心天文基準系(GCRS)における座標またはフレーム。 |
|
天体中間参照系(CIRS)における座標またはフレーム。 |
|
国際地球基準系(ITRS)における座標またはフレーム。 |
|
日心座標系における座標またはフレームは,その軸がICRSと整列する. |
|
真赤道均等フレーム(TEME)における座標またはフレーム。 |
|
真赤道と真分点(TETE)の赤道座標やフレームを用いる. |
|
GCRと同様の方法で定義された座標フレームは、要求された(平均)分点に進むが、それは要求された(平均)分点に進む。 |
|
地心平均黄道座標。 |
|
重心平均黄道座標。 |
|
日心平均黄道座標。 |
|
地心真黄道座標。 |
|
重心真黄道座標。 |
|
日心真黄道座標。 |
|
ある特定の位置に対してそのフレームにマッチするフレームとして位置付けられる. |
|
ローカル静止基準(LSR)における座標またはフレーム、軸と |
|
ローカルREST規格(LSR)における座標またはフレーム。 |
|
運動学的局所静止基準(LSR)における座標またはフレーム。 |
|
RESTの動的ローカル標準(LSRD)における座標またはフレーム |
|
黄道フレームの名前と約束されたフレームに類似した基底クラスを持つ. |
|
典型的な“赤道”約束に従って経度および緯度を右揚角および赤緯度として表すフレームのデフォルト表現情報を定義する基本クラス。 |
|
日心平均(IAU 1976)黄道座標。 |
|
重心黄道座標とカスタム傾斜角。 |
参照/API¶
AXTYPY.COLISTESパッケージ¶
このサブパッケージは、天文オブジェクトの天文座標のクラスと関数を含む。これはまた,座標系間で変換するためのフレームワークを含む.
機能¶
|
球面上の2点間の角度間隔。 |
|
3次元直角デカルト座標を球極座標に変換する. |
|
複数の座標オブジェクトを1つに統合する |
各コンポーネント内のデータを接続することにより、複数の表現オブジェクトを単一のインスタンスに統合する。 |
|
|
|
|
太陽系天体の重心位置を計算する。 |
|
太陽系天体の質量心の位置と速度を計算する。 |
|
与えられた座標オブジェクトに含まれるコンステレーションを決定する。 |
|
オンライン名前解析サービスを用いて指定された名前の座標を検索することでICRSオブジェクトを検索する. |
|
|
|
所与の時間(アレイが入力されている場合、1つまたは複数の時間)の太陽の位置を決定する |
|
フィボナチや黄金螺旋法を用いて単位球体の曲面上に点のグリッドを生成する. |
|
利用可能な変換および座標系を表示する変換マップを含むように、他の文書文字列で使用可能な文字列を生成する。 |
|
ディレクトリ座標のセットにおいて、1つまたは複数の座標に最も近い3次元マッチングアイテムが検索される。 |
|
ディレクトリ座標のセットにおいて、1つまたは複数の座標に最も近い空一致が検索される。 |
|
距離所与の点は、所与のオフセットを有する点を有する。 |
|
球体上の2点間の位置角度(北方向以東)。 |
|
3次元空間において少なくとも指定された距離と同じ近い点対を探索する. |
|
探索角度間隔は,少なくとも指定された角度の点対に近い. |
|
球面極座標を直角デカルト座標に変換する. |
|
単位球体曲面上の点のランダムサンプリングを生成する. |
|
球内に均一な体積密度分布に従う点のランダムサンプリングを生成する。 |
クラス¶
|
3 x 3デカルト変換行列と変位ベクトルタプルを生成する関数として座標変換を指定する. |
高さ−方位角系ではWS 84に対するスフェロイドの座標やフレーム(水平座標)である。 |
|
|
単位がアークまたは度数に等しい1つまたは複数の角度値。 |
|
フレーム属性の不変データ記述子を保存する. |
|
重心平均黄道座標。 |
|
重心真黄道座標。 |
|
コントロール間の汎用機能の基本クラス |
|
座標枠の基底類。 |
|
差異を表す基底クラスを表す. |
|
黄道フレームの名前と約束されたフレームに類似した基底クラスを持つ. |
|
基準大地表示法。 |
|
典型的な“赤道”約束に従って経度および緯度を右揚角および赤緯度として表すフレームのデフォルト表現情報を定義する基本クラス。 |
|
3次元座標系では点の基準を表す. |
|
3次元座標は和差分を表す. |
|
球形ベースで表される点との違い. |
|
|
角度がユーザが指定した限界を超えた場合に開始される。 |
|
|
天体中間参照系(CIRS)における座標またはフレーム。 |
|
点は3次元デカルト座標における微分である. |
|
点は3次元デカルト座標で表される. |
|
フレーム属性は,指定された単位を持つデカルト表現法である. |
|
一連の単ステップ変換を組み合わせることで構造された変換. |
一方の座標系が他の座標系に変換できない場合には、開始される |
|
|
フレーム属性は,座標オブジェクトである. |
|
座標を1つのシステムから別のシステムのオブジェクトに変換する. |
|
重心黄道座標とカスタム傾斜角。 |
|
円柱座標の中点の微分. |
|
点は3 D柱面座標で表される。 |
|
フレーム属性は、差分インスタンスである。 |
|
一次元距離です。 |
|
関数として指定された座標変換は,3 x 3デカルト変換行列を生成することができる. |
|
地球上の位置です |
|
役割を果たすことができる |
|
FK 4システムにおける座標またはフレーム. |
|
FK 4システムでは座標またはフレームであるが,収差のE項は除去されている. |
|
FK 5システムにおける座標またはフレーム。 |
|
座標オブジェクトを受け取り変換後の座標オブジェクトを返す関数で定義される座標変換. |
|
座標変換の働き方は |
|
地心天文基準系(GCRS)における座標またはフレーム。 |
|
GRS 80は3次元大地座標の中点の表示である。 |
|
銀河座標系における座標やフレームです |
|
ローカル静止基準(LSR)における座標またはフレーム、軸と |
|
銀河系の座標やフレームです |
|
1つのFrameオブジェクトは,データを格納することはできないが,任意のFrame属性を保存することができる. |
|
地心平均黄道座標。 |
|
地心真黄道座標。 |
|
日心座標系における座標またはフレームは,その軸がICRSと整列する. |
|
日心平均(IAU 1976)黄道座標。 |
|
日心平均黄道座標。 |
|
日心真黄道座標。 |
|
ICRSシステムにおける座標またはフレーム. |
|
国際地球基準系(ITRS)における座標またはフレーム。 |
|
時間値が[0,24]の範囲内にない場合に開始される. |
|
タイム値が24の場合に開始される. |
|
分値がその範囲内にない場合には [0,60] それがそうです。 |
|
分値が60の場合に発生する. |
|
2番目の値(時間)がその範囲内にない場合に開始される [0,60] それがそうです。 |
|
2番目の値が60である場合に開始される。 |
|
ローカルREST規格(LSR)における座標またはフレーム。 |
|
RESTの動的ローカル標準(LSRD)における座標またはフレーム |
|
運動学的局所静止基準(LSR)における座標またはフレーム。 |
|
-90から+90度の範囲の類似緯度の角度でなければならない。 |
|
連続する360度の範囲で包まれた経度状の角度。 |
|
物理的に約束された3 D球面座標の微分を用いる. |
|
3次元球座標に点を表示する(使用する物理的約束 |
|
GCRと同様の方法で定義された座標フレームは、要求された(平均)分点に進むが、それは要求された(平均)分点に進む。 |
|
フレーム属性は,指定された単位と形状を持つ数(オプション)である. |
|
半径方向距離の差。 |
|
点から原点までの距離を表す. |
角度の一部がその有効範囲を超えた場合に引き起こされる。 |
|
|
これが…。 |
|
システム間の天体座標表現,操作,変換に柔軟なインタフェースを提供する高度なオブジェクト. |
|
名前、記述、フォーマットなどのメタ情報のコンテナ。 |
|
ある特定の位置に対してそのフレームにマッチするフレームとして位置付けられる. |
|
それぞれの単位のスペクトル座標を持っている。 |
|
スペクトル単位を有する1つ以上の値。 |
|
3 D球面座標中点の微分。 |
|
3 D球面座標中点の微分。 |
|
点は3 D球面座標における表現である. |
|
3 x 3デカルト変換行列の座標変換と定義する. |
|
超銀河座標(Lahavらを参照)2000、<https://ui.adsab.atherard.edu/abs/2000 MNRAS.312..166 L>、およびその中の参考文献)。 |
|
真赤道均等フレーム(TEME)における座標またはフレーム。 |
|
真赤道と真分点(TETE)の赤道座標やフレームを用いる. |
|
時間オブジェクトの量であるフレーム属性記述子. |
|
座標フレーム間の経路を表す図形. |
|
単位球面上の点の微分. |
|
単位球面上の点の微分. |
|
単位球面上の点の表示. |
|
|
|
WGS 72の3次元大地座標の中点を示す。 |
|
WGS 84 3次元大地座標の中点の表示。 |
このような制御は |
|
太陽系天体の位置を計算するためのデフォルト天体暦。 |