ガウス1 D

class astropy.modeling.functional_models.Gaussian1D(amplitude=1, mean=0, stddev=1, **kwargs)

ベースクラス: astropy.modeling.core.Fittable1DModel

1次元ガウスモデルです

パラメータ

振幅.振幅 ：浮動または Quantity それがそうです。浮遊や

ガウスの振幅(ピーク)−正規化輪郭(積分1)に対して振幅=1/(Stddev)とする Np.sqrt(2 Np.pi))

mean ：浮動または Quantity それがそうです。浮遊や

ガウスの平均値。

標準設備. ：浮動または Quantity それがそうです。浮遊や

半値幅=2のガウス分布の標準偏差 標準設備. Np.sqrt(2*np.log(2)).

その他のパラメータ

fixed辞書、オプション

1冊の辞書. {{parameter_name: boolean}} パラメータの大きさはフィッティング過程では変化できない.Trueはパラメータが一定に保たれていることを表す.あるいは、 fixed パラメータの属性を用いることができる.

tiedDICT、オプション

1冊の辞書. {{parameter_name: callable}} ある他のパラメータのパラメータにリンクする.辞書値は，リンク関係を提供する呼び出し可能なオブジェクトである.あるいは、 tied パラメータの属性を用いることができる.

boundsDICT、オプション

1冊の辞書. {{parameter_name: value}} パラメータの上下境界。キーはパラメータ名である.値は長さ2のリストまたはタプルであり，パラメータに必要な範囲を与える.あるいは、 min そして max パラメータの属性を用いることができる.

eqconsリスト、オプション

長さ関数リスト n そのためには eqcons[j](x0,*args) == 0.0 最適化に成功した問題の中で。

ineqconsリスト、オプション

長さ関数リスト n そのためには ieqcons[j](x0,*args) >= 0.0 最適化に成功した問題です

参考

Gaussian2D, Box1D, Moffat1D, Lorentz1D

注意事項

Either all or none of input x, mean and stddev must be provided consistently with compatible units or as unitless numbers.

モデル式：

\[F(X)=A e^{-\frac{\Left(x-x_{0}\right)^{2}{2\sigma^{2}}\]

実例.

>>> from astropy.modeling import models
>>> def tie_center(model):
...         mean = 50 * model.stddev
...         return mean
>>> tied_parameters = {'mean': tie_center}

以下の2つの方式のうちの1つにより“Mean”がバインディングパラメータであることを指定する：

>>> g1 = models.Gaussian1D(amplitude=10, mean=5, stddev=.3,
...                             tied=tied_parameters)

あるいは…。

>>> g1 = models.Gaussian1D(amplitude=10, mean=5, stddev=.3)
>>> g1.mean.tied
False
>>> g1.mean.tied = tie_center
>>> g1.mean.tied
<function tie_center at 0x...>

固定パラメータ：

>>> g1 = models.Gaussian1D(amplitude=10, mean=5, stddev=.3,
...                        fixed={'stddev': True})
>>> g1.stddev.fixed
True

あるいは…。

>>> g1 = models.Gaussian1D(amplitude=10, mean=5, stddev=.3)
>>> g1.stddev.fixed
False
>>> g1.stddev.fixed = True
>>> g1.stddev.fixed
True

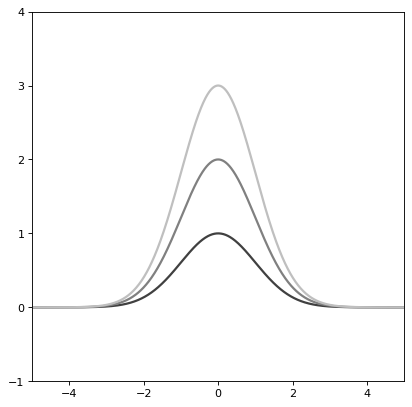
import numpy as np
import matplotlib.pyplot as plt

from astropy.modeling.models import Gaussian1D

plt.figure()
s1 = Gaussian1D()
r = np.arange(-5, 5, .01)

for factor in range(1, 4):
    s1.amplitude = factor
    plt.plot(r, s1(r), color=str(0.25 * factor), lw=2)

plt.axis([-5, 5, -1, 4])
plt.show()

(png, svg, pdf)

属性要約

amplitude \
fwhm \	最大値が半分の場合のガウス全幅.
input_units \	この属性は、Evaluateメソッドがどの単位または単位セットを必要とするかを示し、入力を単位にマッピングする(または)ことを返すために使用される None 任意の単位が受け入れられていれば).
mean \
param_names \	このタイプモデルのパラメータ名を記述する.
stddev \

方法要約

evaluate \(X，振幅，平均，標準偏差)	ガウス一次元モデル関数。
fit_deriv \(X，振幅，平均，標準偏差)	ガウス一次元モデル関数導関数。

属性文書

amplitude = Parameter('amplitude', value=1.0)

fwhm

最大値が半分の場合のガウス全幅.

input_units

mean = Parameter('mean', value=0.0)

param_names = ('amplitude', 'mean', 'stddev')

このタイプモデルのパラメータ名を記述する.

このタプル内のパラメータの順序は、特定のタイプのモデルを初期化する際に入力されるべき順序と同じである。いくつかのタイプのモデル(例えば、多項式モデル)は、次数のようなモデルのいくつかの他の属性に依存する異なる数のパラメータを有する。

モデルクラスを定義する際には，その属性の値は Parameter クラス主体で定義された属性.

stddev = Parameter('stddev', value=1.0, bounds=(1.1754943508222875e-38, None))

方法文書

static evaluate(x, amplitude, mean, stddev)

ガウス一次元モデル関数。

static fit_deriv(x, amplitude, mean, stddev)

ガウス一次元モデル関数導関数。