穏健統計推定量¶

ロバストな統計データは複雑な分布の基本統計データに信頼できる推定を提供する。統計ソフトウェアパッケージは天文学でよく使われるいくつかの強力な統計関数を含む。これは、異常値を除去する方法と、潜在的分布の統計的記述とを含む。

ここで述べた機能に加えて，モデルは以下の方法を用いて異常値除去をフィッティングすることができる. FittingWithOutlierRemoval() それがそうです。

シグマ仕立て¶

Sigmaクロッピングは，分布中の異常値を迅速に識別する方法を提供する。点の分布に対して，中心と標準偏差を計算する.拒否距離中心値は、指定された数の標準偏差の値以下であるか、またはそれ以上である。このプロセスは、グループ外値をさらに拒否するために繰り返されることができる。

♪the astropy.stats Packageはsigmaクロッピングに機能とオブジェクト指向インタフェースを提供する.この関数は呼び出されます sigma_clip() この種類は SigmaClip それがそうです。デフォルトの場合、それらは、拒否された点がマスクされたマスク配列に戻る。

実例.¶

平均値が0，標準偏差が0.2であるが，異常値を持ついくつかのデータを生成することから始めることができる.

>>> import numpy as np
>>> import scipy.stats as stats
>>> np.random.seed(0)
>>> x = np.arange(200)
>>> y = np.zeros(200)
>>> c = stats.bernoulli.rvs(0.35, size=x.shape)
>>> y += (np.random.normal(0., 0.2, x.shape) +
...       c*np.random.normal(3.0, 5.0, x.shape))

今私たちは sigma_clip() データに対してシグマクロッピングを実行するには、以下の操作を実行してください。

>>> from astropy.stats import sigma_clip
>>> filtered_data = sigma_clip(y, sigma=3, maxiters=10)

そして、出力マスク配列を用いてデータの統計データを計算したり、モデルをデータに適合させたり、他の方法でデータを探索したりすることができる。

同じsigmaクロッピングを実行する SigmaClip クラス：

>>> from astropy.stats import SigmaClip
>>> sigclip = SigmaClip(sigma=3, maxiters=10)
>>> print(sigclip)  
<SigmaClip>
   sigma: 3
   sigma_lower: None
   sigma_upper: None
   maxiters: 10
   cenfunc: <function median at 0x108dbde18>
   stdfunc: <function std at 0x103ab52f0>
>>> filtered_data = sigclip(y)

注意してください sigclip 例は、同じ定義されたσクロッピングパラメータを使用して他のデータに適用することができる。

基本的な統計では sigma_clipped_stats() 配列のσトリミング平均値、中央値、および標準偏差を計算するための便利な関数である。拒否異常値は基礎分布の正確な値を返すことが分かる.

使用 sigma_clipped_stats() シグマ仕立ての統計計算では

>>> from astropy.stats import sigma_clipped_stats
>>> y.mean(), np.median(y), y.std()  
(0.86586417693378226, 0.03265864495523732, 3.2913811977676444)
>>> sigma_clipped_stats(y, sigma=3, maxiters=10)  
(-0.0020337793767186197, -0.023632809025713953, 0.19514652532636906)

sigma_clip() そして SigmaClip 改善された群外値拒否を提供するために、他のロバストな統計データと組み合わせることができる。

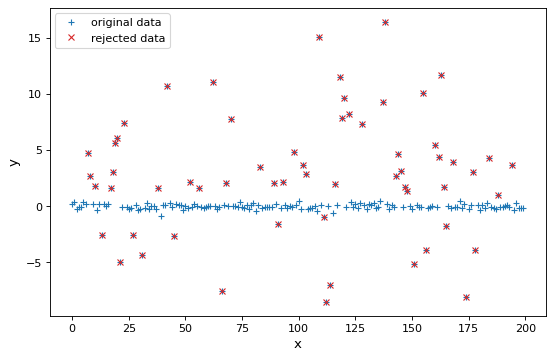
import numpy as np
import scipy.stats as stats
from matplotlib import pyplot as plt
from astropy.stats import sigma_clip, mad_std

# Generate fake data that has a mean of 0 and standard deviation of 0.2 with outliers
np.random.seed(0)
x = np.arange(200)
y = np.zeros(200)
c = stats.bernoulli.rvs(0.35, size=x.shape)
y += (np.random.normal(0., 0.2, x.shape) +
      c*np.random.normal(3.0, 5.0, x.shape))

filtered_data = sigma_clip(y, sigma=3, maxiters=1, stdfunc=mad_std)

# plot the original and rejected data
plt.figure(figsize=(8,5))
plt.plot(x, y, '+', color='#1f77b4', label="original data")
plt.plot(x[filtered_data.mask], y[filtered_data.mask], 'x',
         color='#d62728', label="rejected data")
plt.xlabel('x')
plt.ylabel('y')
plt.legend(loc=2, numpoints=1)

(png, svg, pdf)

Asterpy.stats.sigma_clippingモジュール¶

機能¶

`sigma_clip` \(データ[, sigma, sigma_lower, ...] )	提供されたデータに対してsigma-クロッピングを実行します。
`sigma_clipped_stats` \(データ[, mask, ...] )	提供されたデータのシグマ切り出し統計データを計算する.

クラス¶

SigmaClip \([sigma, sigma_lower, sigma_upper, ...] )

クラスはsigmaクロッピングを実行する.

クラス継承関係図¶

中央値絶対偏差¶

中央値絶対偏差(MAD)は分布拡散に対するメトリックであり，これを定義する. median(abs(a - median(a))) それがそうです。MADは次式で計算できる median_absolute_deviation それがそうです。正規分布では、MADは標準偏差に1.4826倍相関し、便利関数である。 mad_std アプリケーション変換に使用することができる。

注釈

関数は median_absolute_deviation 計算に用いる中央値関数を指定するには、以下の操作を実行してください。NumPyのバージョンおよび配列がブロックされているか不規則な値を含むかによって，中央値関数をあらかじめ選択しておくことで性能を著しく向上させることができる.中央値関数が指定されていなければ median_absolute_deviation 入力データから最も関連する機能の選択を試みる.

双権推定器¶

1組の関数が含まれている. astropy.stats 重量級形式主義のバッグを使います。これらの関数は長い間天文学に用いられてきたが，特に銀河団の速度分散を計算するために用いられてきた. 1. 以下のタスクセットは、二重測定に使用することができる。

Asterpy.stats.biweightモジュール¶

このモジュールは，Tukeyの二重重み関数を用いてロバストな統計データを計算する関数を含む.

機能¶

`biweight_location` \(データ[, c, M, axis, ignore_nan] )	二重物の位置を計算する。
`biweight_scale` \(データ[, c, M, axis, ...] )	二重秤を計算する。
`biweight_midvariance` \(データ[, c, M, axis, ...] )	二重体の中国分散を計算する。
`biweight_midcovariance` \(データ[, c, M, ...] )	多変量対間の二重重みにおける共分散を計算する.
`biweight_midcorrelation` \(X，y[, c, M, ...] )	2つの変数間の双重みにおける相関を計算する.

参考文献¶

1: Beers，FlynnおよびGebhardt(1990；AJ 100，32)(https：//ui.adsab.forforard.edu/abs/1990 AJ...100...32 B)

ナビゲーション