Lomb-Scarger周期図

Lomb-Scarger周期図(Lombの後 1, スカガーと 2) 不均一間隔観測における周期信号を検出するための一般的な統計ツールである。♪the LombScargle クラスはFASTを含むLomb-Scarger周期図のいくつかの実装された統一インタフェースである. [O[NlogN]] Press&Rmbickiによるアルゴリズムの実現 3.

ここのコードは astroml 包装 (4, 5) そして gatspy 包装 (6, 7) それがそうです。Lomb-Scarger周期図の詳細な実践議論については，ベースを用いてください astropy 会いましょう Understanding the Lomb-Scargle Periodogram 11, 関連コードはhttps：//github.com/jakevdp/PracticalLombScarger/にある.

基本的用法

注釈

全ての周波数は LombScargle あります。 not 角度周波数は、発振周波数(すなわち、単位時間当たりのサイクル数)ではない。

Lomb-Scarger周期図は，不均一間隔の観測において周期信号を検出するように設計されている.

例を引く

不均一間隔の観測で周期信号を検出するためには，以下のデータを考える.

>>> import numpy as np
>>> rand = np.random.RandomState(42)
>>> t = 100 * rand.rand(100)
>>> y = np.sin(2 * np.pi * t) + 0.1 * rand.randn(100)

これらは不規則時間で行った100回のノイズ測定であり，周波数は単位時間あたり1周期である。

入力データから自動的に選択された頻度で評価されるLomb-Scarger周期図は以下の方法で計算できる. LombScargle クラス：

>>> from astropy.timeseries import LombScargle
>>> frequency, power = LombScargle(t, y).autopower()

Matplotlibを用いて作成した結果，以下の結果が得られた。

>>> import matplotlib.pyplot as plt  
>>> plt.plot(frequency, power)       

(png, svg, pdf)

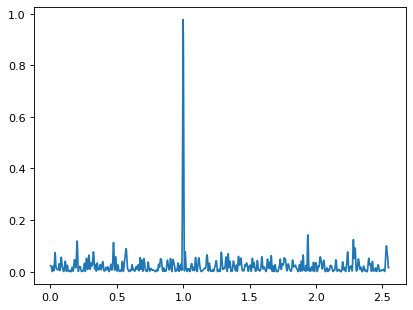
周期図は，構築したデータから予想されるように，周波数が単位時間あたり1周期である明らかなピークを示している.

不確定度を測る

♪the LombScargle インターフェースはまた、測定不確実性を有するデータを処理することができる。

例を引く

すべての不確実性が同じである場合、スカラを渡すことができる：

>>> dy = 0.1
>>> frequency, power = LombScargle(t, y, dy).autopower()

観測によって異なるかどうかが決定されない場合、それらを配列転送とすることができる：

>>> dy = 0.1 * (1 + rand.rand(100))
>>> y = np.sin(2 * np.pi * t) + dy * rand.randn(100)
>>> frequency, power = LombScargle(t, y, dy).autopower()

ガウスの不確実性があると仮定して dy ここでは標準偏差(分散ではない)を指定する.

周期図と単位

♪the LombScargle インタフェース正しく処理する Quantity 単位のオブジェクトを付加し，検証入力を単位が正しいことを確保する.

例を引く

使用する LombScargle 上の Quantity 単位が付着した対象：

>>> import astropy.units as u
>>> t_days = t * u.day
>>> y_mags = y * u.mag
>>> dy_mags = y * u.mag
>>> frequency, power = LombScargle(t_days, y_mags, dy_mags).autopower()
>>> frequency.unit
Unit("1 / d")
>>> power.unit
Unit(dimensionless)

出力は無次元であることが見られ，標準正規化周期図はいつもそうである(正規化に関するより多くの情報は，参照されたい. 周期図正規化 (下記参照)。

周波数を指定する

与 autopower() 方法では，ヒューリスティックアルゴリズムを用いて適切な周波数メッシュを選択する.デフォルトの場合，ヒューリスティック仮説ピーク幅は観測ベースラインに反比例し，最大周波数はいわゆる“平均ナイキスト周波数”の5倍であり，平均観測間隔に基づいて計算される.

このヒューリスティック手法は、不規則サンプリングデータが検出される周波数が平均ナイキスト周波数よりもはるかに高い可能性があるため、一般的に有用ではない。そのため伝達することで autopower() 方法です。

例を引く

使用伝達 autopower() 方法：

>>> frequency, power = LombScargle(t, y, dy).autopower(nyquist_factor=2)
>>> len(frequency), frequency.min(), frequency.max()  
(500, 0.0010189890448009111, 1.0179700557561102)

ここで最高頻度は平均ナイキスト頻度の2倍です。もし私たちが増加すれば nyquist_factor より高い周波数を検出することができます

>>> frequency, power = LombScargle(t, y, dy).autopower(nyquist_factor=10)
>>> len(frequency), frequency.min(), frequency.max()  
(2500, 0.0010189890448009111, 5.0939262349597545)

あるいは私たちは power() 方法：ユーザによって指定された周波数セットで周期図を計算する：

>>> frequency = np.linspace(0.5, 1.5, 1000)
>>> power = LombScargle(t, y, dy).power(frequency)

最も速いLomb-Scargerはルール間隔を必要とする頻度を実現し，周波数間隔が不規則である場合には遅い方法が使用されることに注意されたい.

周波数グリッド間距離

ユーザが周波数を指定する1つの一般的な問題は、有意なピークが格子点の間に位置し、完全に見逃しられるように、あまり太いグリッドが意図的に選択されたことである。

例を引く

周期図を100点で評価することを選択したとしましょう

>>> frequency = np.linspace(0.1, 1.9, 100)
>>> power = LombScargle(t, y, dy).power(frequency)
>>> plt.plot(frequency, power)   

(png, svg, pdf)

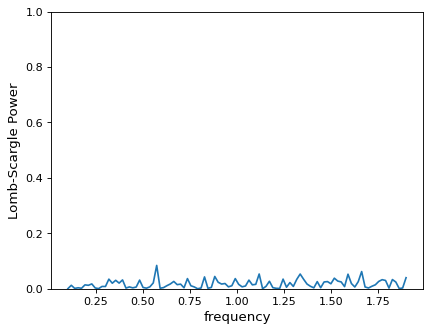
このグラフだけから，データには明らかな周期的な信号は存在しないと結論できる.しかし、この結論は間違っている：実際には強い周期信号が存在するが、周期図ピークは選択された格子点の間の隙間にある！

より信頼できる方法は，周波数ヒューリスティック手法を用いて適切なメッシュ間距離を決定することであり，最小と最大周波数を選択的に伝達することができる. autopower() 方法：

>>> frequency, power = LombScargle(t, y, dy).autopower(minimum_frequency=0.1,
...                                                    maximum_frequency=1.9)
>>> len(frequency)
884
>>> plt.plot(frequency, power)   

(png, svg, pdf)

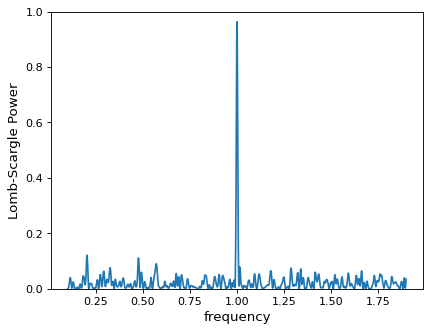
より細かいメッシュ(ここでは0.1から1.9の間の884点)があり，データには非常に強い周期的な信号があることは明らかである.

デフォルトの場合、ヒューリスティックの目標は、各重要な周期グラフピーク上に約5つの格子点があることであり、変更することで samples_per_peak 論点：

>>> frequency, power = LombScargle(t, y, dy).autopower(minimum_frequency=0.1,
...                                                    maximum_frequency=1.9,
...                                                    samples_per_peak=10)
>>> len(frequency)
1767

ピークの幅は観測値のベースラインに反比例し(すなわち、最大と最小時間の差)、必要な格子点の数はベースラインの大きさと線形関係になることを覚えておいてください。

Lomb-Scargerモデル

Lomb-Scarger周期図は周波数ごとのデータに対して正弦波モデルを作成し，パワーが大きいほどフィッティングが良いことを反映している。この点を考慮すると，段階的データ上で最適な正弦曲線を作成することは通常有用である。

例を引く

この最適正弦曲線は model() 方法 LombScargle 目標：

>>> best_frequency = frequency[np.argmax(power)]
>>> t_fit = np.linspace(0, 1)
>>> ls = LombScargle(t, y, dy)
>>> y_fit = ls.model(t_fit, best_frequency)

そしてデータを段階化してLomb-Scarglerモデル適合曲線を描くことができます

(png, svg, pdf)

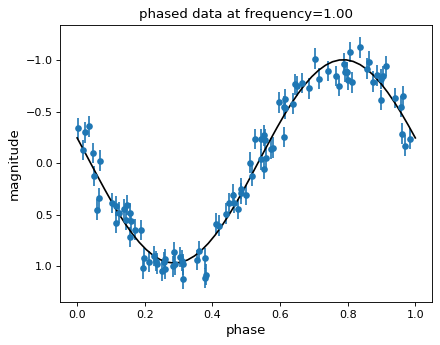
最適適合モデルパラメータは使用可能です model_parameters() 方法 LombScargle 所与の周波数でのオブジェクト：

>>> theta = ls.model_parameters(best_frequency)
>>> theta.round(2)
array([-0.02,  1.05,  0.07])

これらのパラメータは \(\vec{{\theta}}\) 以下のモデルを用いてフィッティングを行う.

\[y(t; f, \vec{\theta}) = \theta_0 + \sum_{n=1}^{\tt nterms} [\theta_{2n-1}\sin(2\pi n f t) + \theta_{2n}\cos(2\pi n f t)]\]

これらのパラメータに基づいて関連を計算することで offset() これはデータの予居中を示しています center_data パラメータ)、および design_matrix() 正弦と余弦項を計算してくれます

>>> offset = ls.offset()
>>> design_matrix = ls.design_matrix(best_frequency, t_fit)
>>> np.allclose(y_fit, offset + design_matrix.dot(theta))
True

その他のパラメータ

初期化時には LombScargle いくつかの制御データモデルの追加パラメータを受け取ります：

• center_data (True by default) controls whether the y values are pre-centered before the algorithm fits the data. The only time it is really warranted to change the default is if you are computing the periodogram of a sequence of constant values to, for example, estimate the window power spectrum for a series of observations.

• fit_mean (True by default) controls whether the model fits for the mean of the data, rather than assuming the mean is zero. When fit_mean=True, the periodogram is more robust than the original Lomb-Scargle formalism, particularly in the case of smaller sample sizes and/or data with nontrivial selection bias. In the literature, this model has variously been called the date-compensated discrete Fourier transform, the floating-mean periodogram, the generalized Lomb-Scargle method, and likely other names as well.

• nterms (1 by default) controls how many Fourier terms are used in the model. As seen above, the standard Lomb-Scargle periodogram is equivalent to a single-term sinusoidal fit to the data at each frequency; the generalization is to expand this to a truncated Fourier series with multiple frequencies. While this can be very useful in some cases, in others the additional model complexity can lead to spurious periodogram peaks that outweigh the benefit of the more flexible model.

周期図正規化

There are several normalizations of the Lomb-Scargle periodogram found in the literature. LombScargle makes four options available via the normalization argument: normalization='standard' (the default), normalization='model', normalization='log', and normalization='psd'. These normalizations can be thought of in terms of least-squares fits around a constant reference model \(M_{ref}\) and a periodic model \(M(f)\) at each frequency, with best-fit sum of residuals that we will denote by \(\chi^2_{ref}\) and \(\chi^2(f)\) respectively.

標準正規化

デフォルトの場合、標準規格化周期図は、定常参照モデルの周囲のデータ残差によって規格化される。

\[P_{STANDARD}(F)=\frac{\chi^2_{ref}-\chi^2(F)}{\chi^2_{ref}}\]

この形の規範化は (normalization='standard' )は、使用中のデフォルトオプションです LombScargle それがそうです。そこから生まれる力は P 範囲内にある無量綱量です 0≦P≦1 それがそうです。

モデル正規化

あるいは、周期図は、周期モデルの周囲の残差によって規格化される場合がある：

\[P_{model}(F)=\frac{\chi^2_{ref}-\chi^2(F)}{\chi^2(F)}\]

この形式の規格化は normalization='model' それがそうです。上述したように、生成された累乗は、その範囲内に位置する無次元量である。 0≦P≦∞ それがそうです。

対数正規化

もう1つの標準化形式は、対数収縮周期図である。

\[P_{log}(F)=\log\frac{\chi^2_{ref}{\chi^2(F)}\]

この正規化は用いることができる normalization='log' 得られたべき乗は範囲内の無次元量です 0≦P≦∞ それがそうです。

PSD規格化(非規格化)

最後に，非正規化周期図を計算することも有用である場合がある. (normalization='psd' )：

\[P_{PSD}(F)=\frac{1}{2}\Left(\chi^2_{ref}-\chi^2(F)\right)\]

不確定な場合には単位があることになる y.unit ** 2 それがそうです。この正規化構造は、標準的なフーリエ電力スペクトル密度(PSD)に相当するように構成されている。

>>> ls = LombScargle(t_days, y_mags, normalization='psd')
>>> frequency, power = ls.autopower()
>>> power.unit
Unit("mag2")

しかし、注意してください。 normalization='psd' 結果はこれらの単位しかありません 不確実性が指定されていなければ それがそうです。不確実性が存在する場合、未正規化されたPSD周期グラフであっても無量綱となるが、これは、Lomb-Scargler計算において不確実性に基づいてデータをスケーリングするためである。

>>> # with uncertainties, PSD power is unitless
>>> ls = LombScargle(t_days, y_mags, dy_mags, normalization='psd')
>>> frequency, power = ls.autopower()
>>> power.unit
Unit(dimensionless)

非正規化，不確実性の場合，均一サンプリング入力の結果を直接比較することで，PSD正規化周期図とフーリエPSDの等価性が確認できる。

まず、均一サンプリング量の基本的なフーリエ周期図を計算するための便利な関数を定義する。

>>> def fourier_periodogram(t, y):
...     N = len(t)
...     frequency = np.fft.fftfreq(N, t[1] - t[0])
...     y_fft = np.fft.fft(y.value) * y.unit
...     positive = (frequency > 0)
...     return frequency[positive], (1. / N) * abs(y_fft[positive]) ** 2

次に、均一にサンプリングされたデータからPSDの2つのバージョンを計算します。

>>> t_days = np.arange(100) * u.day
>>> y_mags = rand.randn(100) * u.mag
>>> frequency, PSD_fourier = fourier_periodogram(t_days, y_mags)
>>> ls = LombScargle(t_days, y_mags, normalization='psd')
>>> PSD_LS = ls.power(frequency)

検査結果を見ると2つの出力が一致しています

>>> u.allclose(PSD_fourier, PSD_LS)
True

この等価性は，Lomb-Scarger周期図がフーリエパワースペクトル密度(PSD)の拡張の原因の1つと考えられていることである.

これらの正規化された統計属性に関するより多くの情報、例えば、Baluev 2008を参照 8.

ピーク有意性と虚警告確率

注釈

Lomb−Scargleピークの重要性を虚警告確率で解釈することは微妙な課題であり，以下の計算量は通常誤解や誤用される。周期図のピーク重要性に関する詳細な検討は、参照されたい 11.

Lomb-Scarger周期グラフを用いて信号に周期成分が含まれているかどうかを判断する場合，重要な考慮要因の1つは周期グラフピークの重要性である.このような重要性は、一般に、周期成分のないガウス雑音からなると仮定して、所与の高さ(またはそれ以上)のピークの確率を測定する仮想警告確率で表される。

例を引く

Lomb-Scarger周期図を用いて我々の信号に周期成分が含まれているかどうかを決定するためには，60個のノイズ付き正弦波観測をシミュレートすることから始めることができる.

>>> t = 100 * rand.rand(60)
>>> dy = 1.0
>>> y = np.sin(2 * np.pi * t) + dy * rand.randn(60)
>>> ls = LombScargle(t, y, dy)
>>> freq, power = ls.autopower()
>>> print(power.max())  
0.33814001958188855

周期図のピークは0.33であるが，このピークはどのくらい重要であろうか。私たちは使用することができます false_alarm_probability() 方法：

>>> ls.false_alarm_probability(power.max())  
0.0043217866919174324

このことは，データに周期信号がないという仮定の下で，このような高いピークが約0.4%の時間で観察されることを示しており，データ中に周期信号が存在することを強く示している.

注釈

ユーザはこの確率をよく説明しなければなりません無信号のゼロ仮説を条件として測定されます記号ではこのように書くことができます \(P({{\rm data}} \mid {{\rm noise-only}})\) それがそうです。

この量は一言で説明できるように見えるが，例えば“このデータは0.4%の可能性はノイズである”というように見えるが，実際には not 正確な陳述 \(P({{\rm noise-only}} \mid {{\rm data}})\) そして一般的には \(P(A\mid B) \ne P(B\mid A)\) それがそうです。

見 11 このような警告のより詳細な議論については、参照されたい。

任意の仮想警告確率を達成するために必要なピーク高さを計算したいかもしれません false_alarm_level() 方法：

>>> probabilities = [0.1, 0.05, 0.01]
>>> ls.false_alarm_level(probabilities)  
array([0.25446627, 0.27436154, 0.31716182])

このことは，10%の虚警告確率を達成するためには，最高周期グラフピークに約0.25，5%に0.27，1%に0.32を要することを示している.

虚警近似.

いずれの特定の頻度でも虚警告確率は解析的に計算可能であるが，閉じた形の解析式では表現されていない. 最高値. 特定の周期図ではピークに達する。これはBootstrapシミュレーションによって決定されるか，様々な方法で近似されなければならない.

astropy 仮想警告確率に近い4つのオプションを提供しており、ご利用いただけます method キーワード：

• method="baluev" Baluev 2008によって提案された近似値を実現する(デフォルト) 8, これは極値統計を用いてエイリアシングなしの虚警告確率の上界を計算する.実験により，高度にエイリアシングされた観測パターンに対してもこの境界が有用であることが分かった.

>>> ls.false_alarm_probability(power.max(), method='baluev')  
0.0043217866919174324

• method="bootstrap" 同一観測時間内のシミュレーションデータを効率的に計算した複数のLomb-Scarger周期図をBootstrapシミュレーションを実現した.Bootstrap方法は仮想警告確率を非常に正確に決定することができるが、計算は非常に高価である。虚警確率に対応するレベルを見積もるには、以下の操作を実行してください \(P_{{false}}\) 注文する必要があります。 \(n_{{boot}} \approx 10/P_{{false}}\) データセットで計算された各周期図である.

>>> ls.false_alarm_probability(power.max(), method='bootstrap')  
0.0030000000000000027

• method="davies" Baluev法と関係があるが，大きな虚警報確率では正確性が失われる。

>>> ls.false_alarm_probability(power.max(), method='davies')  
0.0043311525763707216

• method="naive" 周期グラフにおいて良好な領域を分離することが独立であるという仮定に基づく基本的な方法である.一般に，虚警確率の見積りは非常に悪く，実際に用いるべきではないが，完全性のために含まれている.

>>> ls.false_alarm_probability(power.max(), method='naive')  
0.0011693992470136049

以下の図では，100個の観測値のピーク高さ範囲内のこれらの虚警告推定値を重篤に混在した観測パターンと比較した。

(png, svg, pdf)

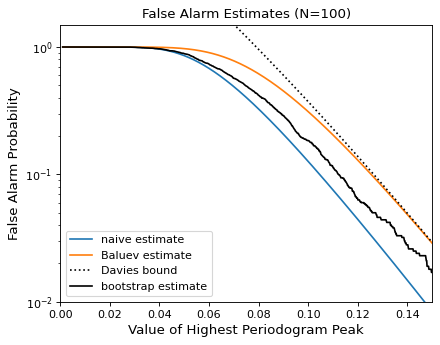
一般に，計算が可能な場合には，ユーザはbootstrap手法を用いるべきであり，そうでなければBaluev手法を用いるべきである.

このすべての中で重要なのはいくつかの警告を覚えておくことです

• 仮想警告確率は、1組の特定の観測時間および特定の周波数メッシュ選択に対して計算される。

• 虚警告確率は周期成分のないデータのゼロ仮定を条件としており，特にデータが周期モデルと実際に一致するかどうかについては定量的な説明はない.

• 虚警告確率と周期図中の最高ピークは 正しいです。 ピークは，特に強いエイリアシングパターンを持つ観測の場合には特に有用ではない。

誤警報確率を計算·解釈する際のこれらの警告や他の注意事項の詳細については，参照されたい 11.

周期図アルゴリズム

♪the LombScargle クラスはLomb-Scarger周期図のいくつかの補完実現を提供し，利用可能である. method Lomb-Scargerの威力のキーワード。設計により、すべての方法は同じ結果(いくつかの近似)を返し、各方法には長所と短所がある。

たとえば，Palmer(2009)の高速カード側手法を用いて周期グラフを計算する. 9, ご指定いただけます method='fastchi2' ：

>>> frequency, power = LombScargle(t, y).autopower(method='fastchi2')

このパッケージには現在6つの方法があります

method='auto'

♪the auto 方法はデフォルトであり、入力データによって駆動されるヒューリスティック手法を用いて、以下の方法の中から最適なオプションを選択することを試みる。

method='slow'

♪the slow 方法はオリジナルのLomb-Scarger周期図の純粋なPython実装です。 (1, 2) 観測ノイズを考慮して浮動平均値(と呼ばれることがある)を許容する. 広義周期図 じゃあね。 10) それがそうです。この方法は特に速くはなく，そのスケーラビリティはほぼ \(O[NM]\) 上の \(N\) データ点と \(M\) 周波数です。

method='cython'

♪the cython 手法は同じアルゴリズムのCythonで実現されており，このアルゴリズムは method='slow' それがそうです。これは純粋なPythonよりも少し高速に実現されていますが、入力サイズが増加するにつれてメモリ効率が高くなります。計算割合は \(O[NM]\) 上の \(N\) データ点と \(M\) 周波数です。

method='scipy'

♪the scipy 方法は原始Lomb-Scarger周期図を実装したCで実現可能である. scipy.signal.lombscargle() それがそうです。この比は slow 方法は、データまたは拡張(例えば、浮動平均値)にエラーが生じることは許されない。割合は約 \(O[NM]\) 上の \(N\) データ点と \(M\) 周波数です。

method='fast'

♪the fast 方法はPress&Rmbicki高速サイクル図の純粋なPython実装です 3. これは1つの 外押し. 高速フーリエ変換を用いて周期図周波数を近似する方法。まるで slow 方法は，データ誤りと浮動小数点平均値を扱うことができる.割合は約 \(O[N\log M]\) 上の \(N\) データ点と \(M\) 周波数です。高速アルゴリズムは精度と速度を交換し，実周期図に非常に近い結果を生成する.特に、場合によっては、あなたはゼロ未満のべき乗が観察されるかもしれない。

method='chi2'

♪the chi2 方法は行列代数に基づく純粋なPython実装です(参照 7) それがそうです。これは，周波数ごとのLomb-Scarger周期図が正弦曲線対データの最小二乗フィッティングに相当することを利用している.その利点は chi2 方法は周期図を複数のフーリエ項に拡張することを可能にします nterms パラメータです。標準的な問題ではその速度は method='slow' 拡張することができます \(O[n_fNM]\) 上の \(N\) データポイントは \(M\) 周波数と \(n_f\) フーリエ項です。

method='fastchi2'

Palmer(2009)のクイックキャスト方法 9 同じように chi2 手法は，行列はFFTに基づく手法を用いて構成されており，類似している. fast 方法です。結果は比較的効果的な周期図です fast 方法)は，複数の項に拡張することができる.割合は約 \(O[n_f(M + N\log M)]\) 上の \(N\) データポイントは \(M\) 周波数と \(n_f\) フーリエ項です。

要約.要約

以下の表に上記アルゴリズムの機能をまとめる.

方法	計算スケーリング.	不確実性を観測する	偏差項(浮動平均値)	多項条項
"slow"	\(O[NM]\)	はい、そうです。	はい、そうです。	違います。
"cython"	\(O[NM]\)	はい、そうです。	はい、そうです。	違います。
"scipy"	\(O[NM]\)	違います。	違います。	違います。
"fast"	\(O[N\log M]\)	はい、そうです。	はい、そうです。	違います。
"chi2"	\(O[n_fNM]\)	はい、そうです。	はい、そうです。	はい、そうです。
"fastchi2"	\(O[n_f(M + N\log M)]\)	はい、そうです。	はい、そうです。	はい、そうです。

計算スケール列では \(N\) データポイントの数です \(M\) 周波数数であり \(n_f\) 多項フィッティングのフーリエ項数です

RR天琴座例

次の図に，よりリアルなデータセットのための計算周期図の例を示す.ここでのデータには、単純な正弦波よりも光曲線形状が複雑なR型天琴座変星の50回の夜間観測が含まれている。

(png, svg, pdf)

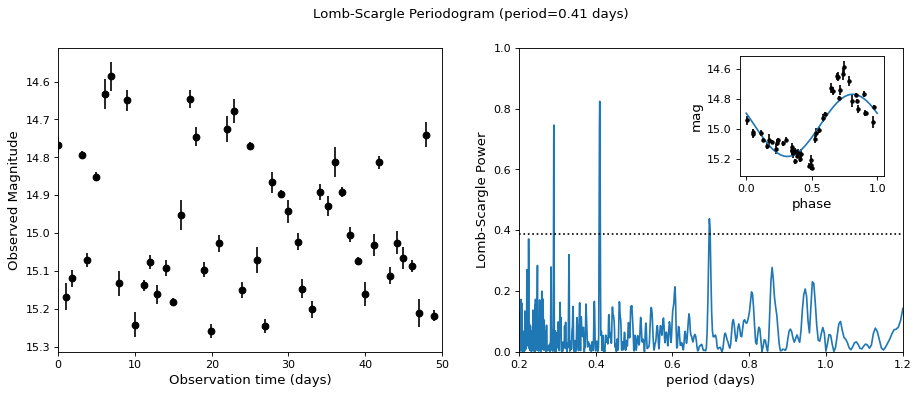
破線は1%の最大ピーク虚警告確率に対応する周期グラフレベルを表す.この例は、不規則にサンプリングされたデータの場合、Lomb−Scargle周期マップは、平均ナイキスト周波数よりも高い周波数に敏感である可能性があることを示している：上記のデータは、平均毎晩1回の観測レートでサンプリングされ、周期マップは、0.41 dの実際の周期を比較的明確に示している。この例では、Lomb−Scargler周期マップは、平均ナイキスト周波数よりも高い頻度に非常に敏感である：上記のデータは、平均毎晩1回サンプリングされ、周期図は、0.41 dの真の周期を比較的明確に示している。

それにもかかわらず、周期図には多くの偽ピークがあり、これは以下のいくつかの要因によるものである。

1. 観測中の誤差は真の山からエネルギーが漏れてしまう。

2. 信号は完璧な正弦波信号ではないので、追加のピークは、信号中のより高い周波数成分を示すことができる。

3. 観測は夜間にのみ行われ，これは測定窓が無視できない電力を持ち，周波数が1日1サイクルであることを意味する。そこで私たちは別名が \(f_{{\rm alias}} = f_{{\rm true}} + n f_{{\rm window}}\) 整数値上 \(n\) それがそうです。観測ウィンドウに0.41日の真の周期と1日の信号がある場合， \(n=+1\) そして \(n=-1\) 別名の周期はそれぞれ0.29日と0.69日であった：これらのエイリアスは上図に顕著に示されている。

これらの効果の相互作用は，実際には，最も高いピークが最良の周波数に対応することは絶対に保証されず，結果は詳細に説明しなければならないことを意味する.これらの影響に関する詳細な議論は、参照されたい 11.

文献参考文献

1(1,2)

ノースカロライナ州レンブ市 Least-squares frequency analysis of unequally spaced data それがそうです。AP&SS 39ページ、447-462ページ(1976)

2(1,2)

スカガーJ.D. Studies in astronomical time series analysis. II - Statistical aspects of spectral analysis of unevenly spaced data それがそうです。APJ 1：263 pp.835-853(1982)

3(1,2)

W.H.とRabicki，G.B. 不均一サンプリングデータスペクトル分析の高速アルゴリズム それがそうです。APJ 1：338，277ページ(1989)

4

トップページ--定期刊行物の主な分類--定期刊行物の詳細紹介--定期刊行物の題録とダイジェスト--定期刊行物の詳細なダイジェスト内容 Astar ML概要：天体物理学における機械学習 それがそうです。知的データ理解会議論文集(2012年)

5

Vanderplas, J., Connolly, A. Ivezic, Z. & Gray, A. Statistics, Data Mining and Machine Learning in Astronomy. Princeton Press (2014)}

6

Vanderplas J. Gatspy：Python天文時系列汎用ツール (2015年)https：//zenodd.org/record/14833

7(1,2)

ファンデルプラスJ&Ivezic Z 多帯域天文時系列の周期図 それがそうです。APJ 812.1：18(2015年)

8(1,2)

房地美巴ルエフ(Baluev，R.V.) 周期図峰の統計的意義を評価する MNRAS 385，1279(2008)

9(1,2)

Palmer D. A Fast Chi-squared Technique for Period Search of Irregularly Sampled Data それがそうです。アジア太平洋地域695.1：496(2009年)

10

Zechmeister MとKurster M The generalised Lomb-Scargle periodogram. A new formalism for the floating-mean and Keplerian periodograms ，A&A 496，577-584(2009)

11(1,2,3,4,5)

Vanderplas J. Understanding the Lomb-Scargle Periodogram ApJS 236.1：16(2018年)https：//ui.adsab.atherard.edu/abs/2018 ApJS...236...16 V