ボックス最小二乗(BLS)サイクルマップ

“ボックス最小二乗”(BLS)サイクルマップ 1 時系列光度データ中の凌日惑星と食双星を検出するための統計ツールである。この実現の主なインタフェースは BoxLeastSquares 級友たち。

数学的背景

BLS方法は、中継を4つのパラメータ(周期、持続時間、深さ、および基準時間)を有する周期的な転置帽子としてモデル化することによって、候補中継を探す。この実装では、基準時間は、ベースラインにおける最初の凌日を観測する中点時間として選択される。これらのパラメータを図に示す.

(png, svg, pdf)

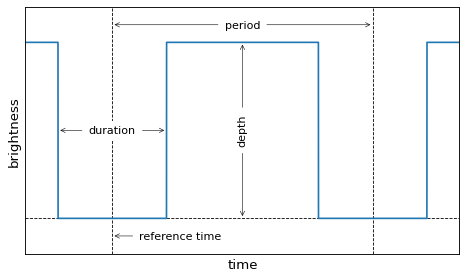
測定トラヒックの不確実性が既知で独立してガウスであると仮定すると，輸送中のトラヒックの最尤は以下のように計算できる.

\[Y_\mathm{in}=\frac{\sum_\mathm{in}y_n/{\sigma_n}^2}{\sum_{mathm{in}1/{\sigma_n}^2}\]

どこだ？ \(y_n\) 輝度測定値です \(\sigma_n\) 関連する不確定要素であり，この2つの総和はいずれも経由数拠点で計算される.

同様に最大可能な輸送外流量は

\[Y_\mathm{out}=\frac{\sum_\mathm{out}y_n/{\sigma_n}^2}{\sum_{out}1/{\sigma_n}^2}\]

このうちこれらの金額は凌日観測を超えている。これらの結果を用いて，輸送モデル(深さ最大化)の所与の期間における対数尤度 \(P\) 持続時間は \(\tau\) 参考時間と \(t_0\) はい。

\[\log\Mathcal{L}(P，\，\tau，\，t_0)= -\frac{1}{2}\，\sum_\mathm{in}\frac{(y_n-y_\mathm{in})^2}{{\sigma_n}^2} -\frac{1}{2}\，\sum_\mathm{out}\frac{(y_n-y_\mathm{out})^2}{{\sigma_n}^2} +\mathm{定数}\]

この方程式は“カイ二乗”に比例するのでよく知っているかもしれない。 \(\chi^2\) このモデルに対して，これは我々が仮定したガウス不確実性の直接的な結果である.

これが…。 \(\chi^2\) “信号残留物”と呼ばれています 1, したがって，持続時間と基準時間の対数尤度を最大化することは，以下の位置からボックス最小二乗スペクトルを計算することに等しい. 1.

実際には、これは、持続時間および基準時間の最尤モデルをメッシュ上で探索することによって実現される。 durations そして oversample のパラメータです。 power 方法です。

舞台裏では，観測データをあらかじめ次の細かいメッシュに結び付けておくことで，必要な計算回数を最大限に削減することを実現している. 1 そして 2.

基本的用法

中継周期図は時系列観測値を入力とし，その中でタイムスタンプをとる. t そして観察されたのは y (通常輝度)は、 numpy アレイや Quantity 物体です。もし知っていたら、間違った条 dy 選択的に提供することも可能である.

例を引く

シミュレーションデータセットの周期図を評価するためには、以下の操作を実行してください。

>>> import numpy as np
>>> import astropy.units as u
>>> from astropy.timeseries import BoxLeastSquares
>>> np.random.seed(42)
>>> t = np.random.uniform(0, 20, 2000)
>>> y = np.ones_like(t) - 0.1*((t%3)<0.2) + 0.01*np.random.randn(len(t))
>>> model = BoxLeastSquares(t * u.day, y, dy=0.01)
>>> periodogram = model.autopower(0.2)

の出力 astropy.timeseries.BoxLeastSquares.autopower 方法は1つです BoxLeastSquaresResults いくつかの有用な属性を持つオブジェクトであり，その中で最も有用な属性は通常 period そして power 属性です。

この結果は、matplotlibを使用してプロットすることができる：

>>> import matplotlib.pyplot as plt                  
>>> plt.plot(periodogram.period, periodogram.power)  

(png, svg, pdf)

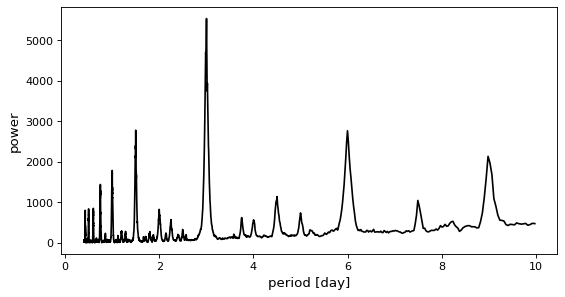
この図では、正しい3日間の期間でピークに達していることが分かる。

目標.目標

デフォルトの場合、 power 方法：モデルフィッティングの対数尤度を計算し、参照時間と持続時間を最大化する。目的関数として、中継深さを測定する信号対雑音比を使用することもできる。

例を引く

モデルフィッティングの対数尤度を計算するには、呼び出してください power あるいは…。 autopower 使用 objective='snr' 詳細は以下のとおりである.

>>> model = BoxLeastSquares(t * u.day, y, dy=0.01)
>>> periodogram = model.autopower(0.2, objective="snr")

(png, svg, pdf)

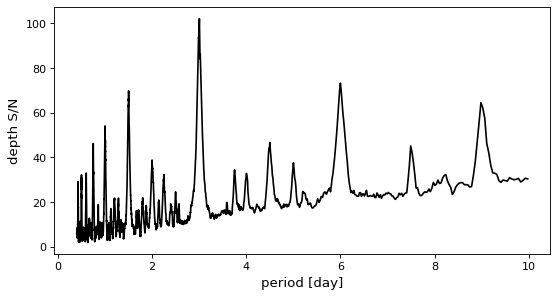
この目標は、一般に、対数尤度スペクトルと定性的に類似した周期マップを生成するが、関連ノイズが存在する場合にバス検索の信頼性を向上させるために使用されている。

周期グリッド

経緯計周期図は常に周期メッシュ上で計算され、結果はサンプリングに敏感である可能性がある。中で述べたとおり 1, 縦横計周期図法の性能は周期メッシュに対する感度が周期メッシュに対する感度より高い。 LombScargle 周期図。

輸送周期マップのこのような実装は、必要な周期メッシュを推定するための保守的ヒューリスティック方法を含み、このメッシュは、 autoperiod そして autopower のAPI文書には，方法とこの方法の詳細な情報が与えられている. autoperiod それがそうです。

例を引く

特定の期間グリッドは、以下のように提供することができる。

>>> model = BoxLeastSquares(t * u.day, y, dy=0.01)
>>> periods = np.linspace(2.5, 3.5, 1000) * u.day
>>> periodogram = model.power(periods, 0.2)

(png, svg, pdf)

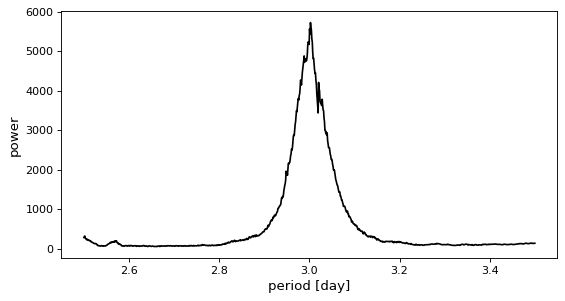
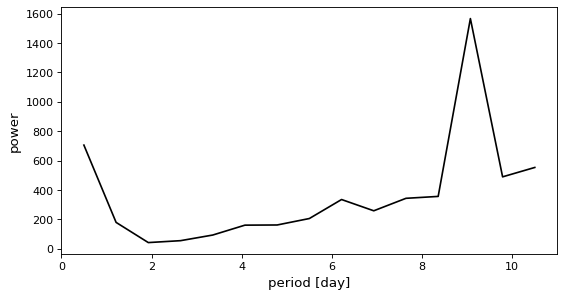
しかし，期間メッシュが太すぎると，正しい期間を逃してしまう可能性がある.

>>> model = BoxLeastSquares(t * u.day, y, dy=0.01)
>>> periods = np.linspace(0.5, 10.5, 15) * u.day
>>> periodogram = model.power(periods, 0.2)

(png, svg, pdf)

ピーク統計情報

通過審査プロセスや候補ピークの調整を支援するために compute_stats 方法は、候補中継の複数の統計情報を計算するために使用することができる。

その多くの統計は中で紹介されたVARTOOLSパッケージに基づいている 2. これは、通常、周期図中の最大点を計算するための統計データであり、以下のようになる。

>>> model = BoxLeastSquares(t * u.day, y, dy=0.01)
>>> periodogram = model.autopower(0.2)
>>> max_power = np.argmax(periodogram.power)
>>> stats = model.compute_stats(periodogram.period[max_power],
...                             periodogram.duration[max_power],
...                             periodogram.transit_time[max_power])

これはこの候補者に関する統計データを含む辞書を計算するだろう。本辞書の見出し語ごとに以下の文書で説明した compute_stats それがそうです。

文献参考文献

1(1,2,3,4,5)

コワッチ、ザック、マゼイ(2002年)、A&A、391，369ページ(arxiv：Astro-ph/0206099)

2(1,2)

ハートマンとバコス(2016年)、天文と計算、17，1(arxiv：1605.06811)