Voigt 1 D

class astropy.modeling.functional_models.Voigt1D(x_0=0, amplitude_L=1, fwhm_L=0.6366197723675814, fwhm_G=0.6931471805599453, method='humlicek2', **kwargs)

ベースクラス: astropy.modeling.core.Fittable1DModel

Voigt断面の一次元モデル。

パラメータ

x_0 ：浮動または Quantity浮遊や

山の峰の位置

amplitude_L ：浮動または Quantity それがそうです。浮遊や

ローレンツ振幅(相関ローレンツ関数のピーク)−正規化輪郭(積分1)に対して，振幅_L=2/(np.pi*fwhm_L)を設定する。

fwhm_L ：浮動または Quantity浮遊や

ローレンツは全幅半高さ

fwhm_G ：浮動または Quantity それがそうです。浮遊や

最大値のガウス全幅

method文字列、オプション

複雑な誤差関数を計算するアルゴリズム；‘Humlicek 2’の1つ(デフォルト、高速かつ通常比 rtol=3.e-5 )や“Scipy”も、“wofz”(必要に応じて)を選択することができます。 scipy ほぼ同じように迅速で正確である)。

その他のパラメータ

fixed辞書、オプション

1冊の辞書. {{parameter_name: boolean}} パラメータの大きさはフィッティング過程では変化できない.Trueはパラメータが一定に保たれていることを表す.あるいは、 fixed パラメータの属性を用いることができる.

tiedDICT、オプション

1冊の辞書. {{parameter_name: callable}} ある他のパラメータのパラメータにリンクする.辞書値は，リンク関係を提供する呼び出し可能なオブジェクトである.あるいは、 tied パラメータの属性を用いることができる.

boundsDICT、オプション

1冊の辞書. {{parameter_name: value}} パラメータの上下境界。キーはパラメータ名である.値は長さ2のリストまたはタプルであり，パラメータに必要な範囲を与える.あるいは、 min そして max パラメータの属性を用いることができる.

eqconsリスト、オプション

長さ関数リスト n そのためには eqcons[j](x0,*args) == 0.0 最適化に成功した問題の中で。

ineqconsリスト、オプション

長さ関数リスト n そのためには ieqcons[j](x0,*args) >= 0.0 最適化に成功した問題です

参考

Gaussian1D, Lorentz1D

注意事項

全部入力するか入力しないか x 位置、位置 x_0 そして fwhm_* 互換性単位は一貫して使用されるか、または単位なし数字として提供されなければならない。Voigt関数は，Schreier 2018(MNRAS 479，3068)に続くHumlicek有理近似(JQSRT 21：309，1979；27：437，1982)により計算された複素誤差関数の実部として計算される. hum2zpf16m 彼のcpfX.pyモジュールから)；または wofz (‘Faddeeva.cc’)を実現します。

実例.

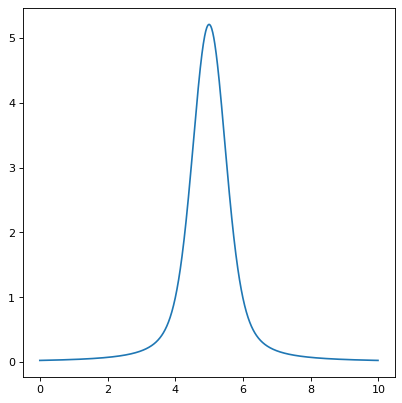
import numpy as np
from astropy.modeling.models import Voigt1D
import matplotlib.pyplot as plt

plt.figure()
x = np.arange(0, 10, 0.01)
v1 = Voigt1D(x_0=5, amplitude_L=10, fwhm_L=0.5, fwhm_G=0.9)
plt.plot(x, v1(x))
plt.show()

(png, svg, pdf)

属性要約

amplitude_L \
fwhm_G \
fwhm_L \
input_units \	この属性は、Evaluateメソッドがどの単位または単位セットを必要とするかを示し、入力を単位にマッピングする(または)ことを返すために使用される None 任意の単位が受け入れられていれば).
param_names \	このタイプモデルのパラメータ名を記述する.
sqrt_ln2 \
sqrt_ln2pi \
sqrt_pi \
x_0 \

方法要約

evaluate (X，x 0，振幅L，fwhm L，fwhm G)	1次元Voigt関数はローレンツピーク振幅にスケーリングされる。
fit_deriv (X，x 0，振幅L，fwhm L，fwhm G)	1次元Voigt関数のパラメータに対する導関数.

属性文書

amplitude_L = Parameter('amplitude_L', value=1.0)

fwhm_G = Parameter('fwhm_G', value=0.6931471805599453)

fwhm_L = Parameter('fwhm_L', value=0.6366197723675814)

input_units

param_names = ('x_0', 'amplitude_L', 'fwhm_L', 'fwhm_G')

このタイプモデルのパラメータ名を記述する.

このタプル内のパラメータの順序は、特定のタイプのモデルを初期化する際に入力されるべき順序と同じである。いくつかのタイプのモデル(例えば、多項式モデル)は、次数のようなモデルのいくつかの他の属性に依存する異なる数のパラメータを有する。

モデルクラスを定義する際には，その属性の値は Parameter クラス主体で定義された属性.

sqrt_ln2 = 0.8325546111576977

sqrt_ln2pi = 1.475664626635606

sqrt_pi = 1.7724538509055159

x_0 = Parameter('x_0', value=0.0)

方法文書

evaluate(x, x_0, amplitude_L, fwhm_L, fwhm_G)

1次元Voigt関数はローレンツピーク振幅にスケーリングされる。

fit_deriv(x, x_0, amplitude_L, fwhm_L, fwhm_G)

1次元Voigt関数のパラメータに対する導関数.