MODELS¶
基礎知識.¶
♪the astropy.modeling Packageは単一の名前空間で収集された多くのモデルを astropy.modeling.models それがそうです。モデルの挙動はパラメータ化関数と類似している:
>>> import numpy as np
>>> from astropy.modeling import models
>>> g = models.Gaussian1D(amplitude=1.2, mean=0.9, stddev=0.5)
>>> print(g)
Model: Gaussian1D
Inputs: ('x',)
Outputs: ('y',)
Model set size: 1
Parameters:
amplitude mean stddev
--------- ---- ------
1.2 0.9 0.5
モデルパラメータは属性としてアクセスすることができる::
>>> g.amplitude
Parameter('amplitude', value=1.2)
>>> g.mean
Parameter('mean', value=0.9)
>>> g.stddev
Parameter('stddev', value=0.5, bounds=(1.1754943508222875e-38, None))
以下の属性で更新することも可能である.
>>> g.amplitude = 0.8
>>> g.amplitude
Parameter('amplitude', value=0.8)
モデルを関数呼び出しとして評価することができる:
>>> g(0.1)
0.22242984036255528
>>> g(np.linspace(0.5, 1.5, 7))
array([0.58091923, 0.71746405, 0.7929204 , 0.78415894, 0.69394278,
0.54952605, 0.3894018 ])
上の例に示すように,一般に,多くのモデルは標準的に類似配列の入力を計算している Numpy broadcasting rules 配列に使います。したがって,モデルはソフトウェアパッケージの実装特性に依存することなく,汎用機能を評価するために有用である(工業·情報化部電子科学技術情報研究所陳胤)
事例化と評価モデル¶
一般に、モデルは、そのモデルのインスタンスを定義するパラメータ値を構造関数に提供することによってインスタンス化される。 パラメータ それがそうです。
さらに1つは Model インスタンスは、パラメータのセットを有する単一のモデルを表すことができ、または Model set 1組のパラメータからなり、各パラメータは同一のパラメータモデルの異なるパラメータ化を表す。例えば、1つの平均値、標準偏差、および振幅を使用して単一のガウスモデルをインスタンス化することができる。代替的に、例えば、画像立方体内の異なる平面上で各ガウス画像を評価するように、N個のガウス画像のセットを作成することができる。
例えば、単一のガウスモデルは、すべてのスカラパラメータを使用してインスタンス化されることができる:
>>> from astropy.modeling.models import Gaussian1D
>>> g = Gaussian1D(amplitude=1, mean=0, stddev=1)
>>> g
<Gaussian1D(amplitude=1., mean=0., stddev=1.)>
新たに作成されたモデル例 g 現在,特定のパラメータを用いた場合,その動作方式はガウス関数に類似している.1つの入力しか受け付けていません
>>> g.inputs
('x',)
>>> g(x=0)
1.0
キーワードパラメータを明示的に使用せずにモデルを呼び出すこともできる:
>>> g(0)
1.0
代替的に、ガウスのセットは、複数のパラメータ値を伝達することによってインスタンス化されてもよい。
>>> from astropy.modeling.models import Gaussian1D
>>> gset = Gaussian1D(amplitude=[1, 1.5, 2],
... mean=[0, 1, 2],
... stddev=[1., 1., 1.],
... n_models=3)
>>> print(gset)
Model: Gaussian1D
Inputs: ('x',)
Outputs: ('y',)
Model set size: 3
Parameters:
amplitude mean stddev
--------- ---- ------
1.0 0.0 1.0
1.5 1.0 1.0
2.0 2.0 1.0
このモデルの動作方式もガウス関数と類似している.同じ入力でモデルセットの3つのモデルを評価することができる:
>>> gset(1.)
array([0.60653066, 1.5 , 1.21306132])
開けたり開いたり N=3 入力:
>>> gset([1, 2, 3])
array([0.60653066, 0.90979599, 1.21306132])
フィッティングモデルセットの総合例については、参照されたい 管部品模型集 それがそうです。
モデル反転¶
すべてのモデルがあります Model.inverse 属性は、いくつかのモデルの場合、その属性は、それが付加されたモデルの解析逆である新しいモデルを返すことができる。例えば:
>>> from astropy.modeling.models import Linear1D
>>> linear = Linear1D(slope=0.8, intercept=1.0)
>>> linear.inverse
<Linear1D(slope=1.25, intercept=-1.25)>
モデルの裏側はつねに完全インスタンス化されたモデルであるため,以下のように直接計算できる.
>>> linear.inverse(2.0)
1.25
1つを カスタマイズ モデルとは逆である.例えば、1つのモデルが逆を解析していないが、数値計算によって別のモデルによって表される近似逆を有する可能性がある場合、これは有用である可能性がある。ターゲットモデルがデフォルトの解析逆を有していても、これは有効である--この場合、デフォルトの解析逆は、カスタム逆によって上書きされる:
>>> from astropy.modeling.models import Polynomial1D
>>> linear.inverse = Polynomial1D(degree=1, c0=-1.25, c1=1.25)
>>> linear.inverse
<Polynomial1D(1, c0=-1.25, c1=1.25)>
カスタマイズされた逆方向をモデルに指定した場合,以下の命令を用いて削除することができる. del model.inverse それがそうです。これは、反転をそのデフォルト値(存在する場合)にリセットする。デフォルト設定が存在しない場合、アクセス model.inverse 1つの問題を引き起こしました NotImplementedError それがそうです。例えば、多項式モデルにはデフォルト逆がない:
>>> del linear.inverse
>>> linear.inverse
<Linear1D(slope=1.25, intercept=-1.25)>
>>> p = Polynomial1D(degree=2, c0=1.0, c1=2.0, c2=3.0)
>>> p.inverse
Traceback (most recent call last):
File "<stdin>", line 1, in <module>
File "astropy\modeling\core.py", line 796, in inverse
raise NotImplementedError("An analytical inverse transform has not "
NotImplementedError: No analytical or user-supplied inverse transform
has been implemented for this model.
しかし,人間はもちろん逆を計算し,多項式モデルに与えることができる.
注釈
カスタム逆をモデルに割り当てる際には,実際に逆であること,さらには近似的な逆であることを保証するために何の検証も行わない.したがって、自己定義反転の危険は自負している。
包囲箱.¶
境界枠付き効率的なモデルレンダリング¶
全部 Model サブクラスは一つあります bounding_box この属性は,モデルの重要な制約を設定するために用いることができる.これは,入力範囲がモデル自体の特徴幅よりもはるかに大きい場合には,評価の効率を大きく向上させる.例えば、大型測定カタログからスカイモデル画像を作成するためには、各ソースが大量のフラックスに寄与する画素のみを評価すべきである。そうでなければ,平均CPU上では,そのタスクは計算上非常に困難である可能性がある.
♪the Model.render 方法は、評価を制限するために、出力配列または入力座標配列上でモデルを評価するために使用することができる bounding_box 領域(設定されている場合)。他の入力配列が渡されていなければ,この関数はモデルの消印画像も生成する.データ配列自体から消印を抽出するように変更しますので、ご参照ください 2 Dクロッピング画像 それがそうです。
ボーダーボックスの使用¶
基本的な用法については参照されたい Model.bounding_box それがそうです。デフォルトの場合はno bounding_box 設定されていますがモデルサブクラスは除外されています bounding_box 属性や方法は明示的に定義されている.そして,デフォルト値はモデルを完全に含む位置の周りで対称な最小矩形領域である.モデルに限られた範囲がなければ,文書には包含基準が明記される.例えば、参照されたい Gaussian2D.bounding_box それがそうです。
Model.bounding_box 呼び出し可能なオブジェクトは、ユーザによって任意に設定されてもよい。これは作成されたモデルを使用するのに特に有用です custom_model あるいは1つとして CompoundModel **
>>> from astropy.modeling import custom_model
>>> def ellipsoid(x, y, z, x0=0, y0=0, z0=0, a=2, b=3, c=4, amp=1):
... rsq = ((x - x0) / a) ** 2 + ((y - y0) / b) ** 2 + ((z - z0) / c) ** 2
... val = (rsq < 1) * amp
... return val
...
>>> class Ellipsoid3D(custom_model(ellipsoid)):
... # A 3D ellipsoid model
... @property
... def bounding_box(self):
... return ((self.z0 - self.c, self.z0 + self.c),
... (self.y0 - self.b, self.y0 + self.b),
... (self.x0 - self.a, self.x0 + self.a))
...
>>> model = Ellipsoid3D()
>>> model.bounding_box
((-4.0, 4.0), (-3.0, 3.0), (-2.0, 2.0))
デフォルトの場合,すべての入力に対してモデルを評価する.フラグを渡すことにより,境界枠内の入力のみを評価する.境界枠以外の入力に対して,a fill_value 戻ります。 (np.nan デフォルトの場合):
>>> model(-5, 1, 1)
0.0
>>> model(-5, 1, 1, with_bounding_box=True)
nan
>>> model(-5, 1, 1, with_bounding_box=True, fill_value=-1)
-1.0
警告
現在、モデルを結合する際に、コンポーネントの境界ブロックは、モデルと & 交換手さん。他の演算子に対しては,複合モデルの境界枠を明示的に指定しなければならない.将来のバージョンは、可能な場合には、複合モデルのための適切な境界ブロックを決定するであろう。
以下の機能により効率的な評価を行う. Model.render()¶
モデル自体よりもはるかに大きい範囲でモデルを評価する際には,慎重に用いる. Model.render 効率性が懸念される場合、使用される。♪the render 方法は、同じ次元数の配列上でモデルを計算するために使用することができる。 model.render() 境界ボックス領域の“消印”に戻るために、パラメータを持たずに呼び出されてもよい。
本例では、2 Dガウスソース100個の300 x 400画素画像を生成する。比較のため,境界枠を用いた場合と用いない場合でモデルの評価を行った.境界フレームを用いることにより,評価速度は約10倍向上したが,情報損失は無視できる.
import numpy as np
from time import time
from astropy.modeling import models
import matplotlib.pyplot as plt
from matplotlib.patches import Rectangle
imshape = (300, 400)
y, x = np.indices(imshape)
# Generate random source model list
np.random.seed(0)
nsrc = 100
model_params = [
dict(amplitude=np.random.uniform(.5, 1),
x_mean=np.random.uniform(0, imshape[1] - 1),
y_mean=np.random.uniform(0, imshape[0] - 1),
x_stddev=np.random.uniform(2, 6),
y_stddev=np.random.uniform(2, 6),
theta=np.random.uniform(0, 2 * np.pi))
for _ in range(nsrc)]
model_list = [models.Gaussian2D(**kwargs) for kwargs in model_params]
# Render models to image using bounding boxes
bb_image = np.zeros(imshape)
t_bb = time()
for model in model_list:
model.render(bb_image)
t_bb = time() - t_bb
# Render models to image using full evaluation
full_image = np.zeros(imshape)
t_full = time()
for model in model_list:
model.bounding_box = None
model.render(full_image)
t_full = time() - t_full
flux = full_image.sum()
diff = (full_image - bb_image)
max_err = diff.max()
# Plots
plt.figure(figsize=(16, 7))
plt.subplots_adjust(left=.05, right=.97, bottom=.03, top=.97, wspace=0.15)
# Full model image
plt.subplot(121)
plt.imshow(full_image, origin='lower')
plt.title(f'Full Models\nTiming: {t_full:.2f} seconds', fontsize=16)
plt.xlabel('x')
plt.ylabel('y')
# Bounded model image with boxes overplotted
ax = plt.subplot(122)
plt.imshow(bb_image, origin='lower')
for model in model_list:
del model.bounding_box # Reset bounding_box to its default
dy, dx = np.diff(model.bounding_box).flatten()
pos = (model.x_mean.value - dx / 2, model.y_mean.value - dy / 2)
r = Rectangle(pos, dx, dy, edgecolor='w', facecolor='none', alpha=.25)
ax.add_patch(r)
plt.title(f'Bounded Models\nTiming: {t_bb:.2f} seconds', fontsize=16)
plt.xlabel('x')
plt.ylabel('y')
# Difference image
plt.figure(figsize=(16, 8))
plt.subplot(111)
plt.imshow(diff, vmin=-max_err, vmax=max_err)
plt.colorbar(format='%.1e')
plt.title(f'Difference Image\nTotal Flux Err = {((flux - np.sum(bb_image)) / flux):.0e}')
plt.xlabel('x')
plt.ylabel('y')
plt.show()
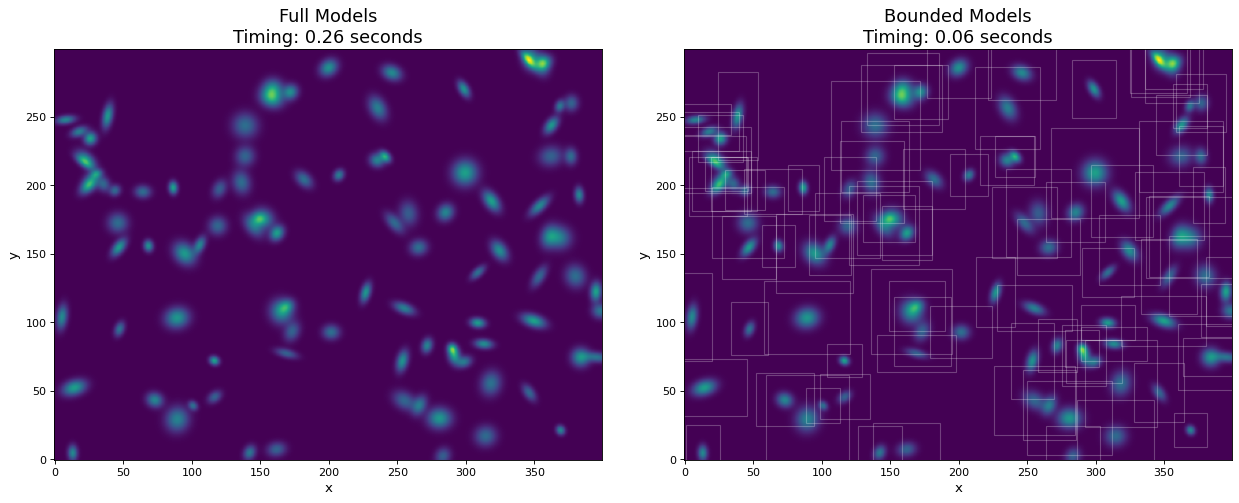

モデル分離性¶
簡単なモデルにはブール値があります Model.separable property. It indicates whether the outputs are independent and is essential for computing the separability of compound models using the is_separable() function. Having a separable compound model means that it can be decomposed into independent models, which in turn is useful in many applications. For example, it may be easier to define inverses using the independent parts of a model than the entire model. In other cases, tools using Generalized World Coordinate System (GWCS) より柔軟で、分離可能なスペクトルおよび空間変換を利用することができる。
模型集.¶
場合によっては、同じタイプであるが異なるパラメータ値セットを有する複数のモデルを記述することが非常に有用である。これはインスタンス化によって可能な限り多くの Model 私たちが必要なように。しかし、多くの車種にとって、これは非効率的かもしれない。そのため,中のすべてのモデルクラスは astropy.modeling モデルを表すためにも利用できます set これは同じタイプのモデルの集合であるが,それらのパラメータ値は異なる.
モデルセットをインスタンス化するには,パラメータを用いてください n_models=N どこだ? N モデルを構築する際の集合中のモデル数である.各パラメータの値は長さリストまたは配列でなければならない N 配列の各々がセット内の1つのモデルに対応するように:
>>> from astropy.modeling import models
>>> g = models.Gaussian1D(amplitude=[1, 2], mean=[0, 0],
... stddev=[0.1, 0.2], n_models=2)
>>> print(g)
Model: Gaussian1D
Inputs: ('x',)
Outputs: ('y',)
Model set size: 2
Parameters:
amplitude mean stddev
--------- ---- ------
1.0 0.0 0.1
2.0 0.0 0.2
これは2つのガウスパラメータに相当する amplitude=1, mean=0, stddev=0.1 そして amplitude=2, mean=0, stddev=0.2 それぞれです。モデルを印刷する際には,パラメータ値をテーブルとして表示し,行ごとに集合中の1つのモデルに対応する.
モデルセットのモデル数は使用可能である len 内蔵::
>>> len(g)
2
個々のモデルの長さは1であるため,モデル集合とはみなさない.
モデルセットを評価する際には,デフォルトの場合,入力長はモデル数と同じでなければならず,モデルごとに1つの入力:
>>> g([0, 0.1])
array([1. , 1.76499381])
その結果,1つの配列であり,集合中の各モデルに1つの結果が得られた.単一の入力値をセットのすべてのモデルにブロードキャストすることもできる:
>>> g(0)
array([1., 2.])
入力が配列である場合:
>>> x = np.array([[0, 0, 0], [0.1, 0.1, 0.1]])
>>> print(x)
[[0. 0. 0. ]
[0.1 0.1 0.1]]
>>> g(x)
array([[1. , 1. , 1. ],
[1.76499381, 1.76499381, 1.76499381]])
内部では,入出力,パラメータ値の形状は属性によって制御される. model_set_axis それがそうです。上記の場合 model_set_axis=0 **
>>> g.model_set_axis
0
これは,0軸に沿った要素が入力として各モデルに渡されることを示している.場合によっては、入力を異なる軸に沿って伝達することが有用である可能性がある:例えば、第1の軸:
>>> x = np.array([[0, 0, 0], [0.1, 0.1, 0.1]]).T
>>> print(x)
[[0. 0.1]
[0. 0.1]
[0. 0.1]]
このモデルには2つのモデルが集中しており,0軸に沿って3つの入力を伝達するため,評価は失敗する.
>>> g(x)
Traceback (most recent call last):
...
ValueError: Input argument 'x' does not have the correct dimensions in
model_set_axis=0 for a model set with n_models=2.
この問題を迂回できる二つの方法がある。 model_set_axis モデルを評価する際に入力することができます
>>> g(x, model_set_axis=1)
array([[1. , 1.76499381],
[1. , 1.76499381],
[1. , 1.76499381]])
または、モデルを初期化する際に、以下の動作を実行する。
>>> g = models.Gaussian1D(amplitude=[[1, 2]], mean=[[0, 0]],
... stddev=[[0.1, 0.2]], n_models=2,
... model_set_axis=1)
>>> g(x)
array([[1. , 1.76499381],
[1. , 1.76499381],
[1. , 1.76499381]])
後者の場合、各パラメータの形状は、現在パラメータが第1の軸に沿って定義されているので、2 Dに変更されていることに留意されたい。
の価値 model_set_axis 異なるパラメータセットと入力を定義する軸を表す整数であってもよいし、値のブール値であってもよい。 False この場合,すべてのモデルセットが評価に同じ入力を用いるべきであることを表す.たとえば,上記のモデルの値は1である. model_set_axis それがそうです。もし model_set_axis=False 伝達後,2つのモデルは同じ入力で値を求める:
>>> g.model_set_axis
1
>>> result = g(x, model_set_axis=False)
>>> result
array([[[1. , 0.60653066],
[2. , 1.76499381]],
[[1. , 0.60653066],
[2. , 1.76499381]],
[[1. , 0.60653066],
[2. , 1.76499381]]])
>>> result[: , 0]
array([[1. , 0.60653066],
[1. , 0.60653066],
[1. , 0.60653066]])
>>> result[: , 1]
array([[2. , 1.76499381],
[2. , 1.76499381],
[2. , 1.76499381]])
現在モデル集は1つのグループを統合するために 線形性. 模型 (example )複数の同じタイプのモデルを同時に(および互いに独立して)いくつかの大きな入力セットに適合させることができ、例えば、データ立方体内の各画素に多項式を適合させる時間応答。これは試着過程を大幅に加速させることができる。加速は,方程式を解くことで正確な解を見つけるためである.反復アルゴリズムを必要とする非線形モデルは現在のところモデル集合を用いてフィッティングすることはできない。非線形モデルのモデル集合しか評価できない.
モデルセットを組み立てる際には,データ配列を正確な形状で組立作業者に渡すことが重要である.形は model_set_axis マッチングするモデルの属性。ルールは,モデル集合に対応する従属変数のインデックスがたどるべきである model_set_axis 次元数.たとえば,3つのモデルを持つ1次元モデル集合に対しては, model_set_axis == 1 その形は y (x,3)::
>>> import numpy as np
>>> from astropy.modeling.models import Polynomial1D
>>> from astropy.modeling.fitting import LinearLSQFitter
>>> fitter = LinearLSQFitter()
>>> x = np.arange(4)
>>> y = np.array([2*x+1, x+4, x]).T
>>> print(y)
[[1 4 0]
[3 5 1]
[5 6 2]
[7 7 3]]
>>> print(y.shape)
(4, 3)
>>> m = Polynomial1D(1, n_models=3, model_set_axis=1)
>>> mfit = fitter(m, x, y)
3つのモデルと model_set_axis = 0 その形は z (3,x,y)::
>>> import numpy as np
>>> from astropy.modeling.models import Polynomial2D
>>> from astropy.modeling.fitting import LinearLSQFitter
>>> fitter = LinearLSQFitter()
>>> x = np.arange(8).reshape(2, 4)
>>> y = x
>>> z = np.asarray([2 * x + 1, x + 4, x + 3])
>>> print(z.shape)
(3, 2, 4)
>>> m = Polynomial2D(1, n_models=3, model_set_axis=0)
>>> mfit = fitter(m, x, y, z)
モデル直列化(モデルをファイルに書き込む)¶
モデルは使えます ASDF フォーマットします。これは多くの文脈で有用であり,その1つは実現である Generalized World Coordinate System (GWCS) それがそうです。
モデルをディスクに直列化することが可能であり,メソッドはオブジェクトを割り当てることである. AsdfFile.tree :
>>> from asdf import AsdfFile
>>> from astropy.modeling import models
>>> rotation = models.Rotation2D(angle=23.7)
>>> f = AsdfFile()
>>> f.tree['model'] = rotation
>>> f.write_to('rotation.asdf')
ファイルを読み込み、モデルを作成するには、以下の操作を実行してください。
>>> import asdf
>>> with asdf.open('rotation.asdf') as f:
... model = f.tree['model']
>>> print(model)
Model: Rotation2D
Inputs: ('x', 'y')
Outputs: ('x', 'y')
Model set size: 1
Parameters:
angle
-----
23.7
Compound models can also be serialized. Please note that some model attributes (e.g meta,
tied parameter constraints used in fitting), as well as model sets are not yet serializable.
For more information on serialization of models, see 細かい点.