組み合わせモデル¶

基礎知識.¶

Astropyモデリングパッケージは定義を new models 既存の関数から、あるいは書くことで Model サブクラス，新しいモデルを作成するもう1つの方法は，算術式を用いてそれらを組み合わせることである.これはAstropyに内蔵されているモデルに適用され，多くのユーザ定義のモデルにも適用可能である.例えば、以下に示すように、2つのガウスの重畳を作成することができる。

>>> from astropy.modeling import models
>>> g1 = models.Gaussian1D(1, 0, 0.2)
>>> g2 = models.Gaussian1D(2.5, 0.5, 0.1)
>>> g1_plus_2 = g1 + g2

生成された対象 g1_plus_2 それ自体が新しいモデルです評価は例えば g1_plus_2(0.25) 評価と同じです g1(0.25) + g2(0.25) **

>>> g1_plus_2(0.25)  
0.5676756958301329
>>> g1_plus_2(0.25) == g1(0.25) + g2(0.25)
True

このモデルは，新たな表現においてさらに他のモデルと結合することができる.

これらの新しい複合モデルは他のモデルの多くのようにデータとフィッティングすることもできます(これは現在非線形適合ツールが必要ですが)：

import numpy as np
import matplotlib.pyplot as plt
from astropy.modeling import models, fitting

# Generate fake data
np.random.seed(42)
g1 = models.Gaussian1D(1, 0, 0.2)
g2 = models.Gaussian1D(2.5, 0.5, 0.1)
x = np.linspace(-1, 1, 200)
y = g1(x) + g2(x) + np.random.normal(0., 0.2, x.shape)

# Now to fit the data create a new superposition with initial
# guesses for the parameters:
gg_init = models.Gaussian1D(1, 0, 0.1) + models.Gaussian1D(2, 0.5, 0.1)
fitter = fitting.SLSQPLSQFitter()
gg_fit = fitter(gg_init, x, y)

# Plot the data with the best-fit model
plt.figure(figsize=(8,5))
plt.plot(x, y, 'ko')
plt.plot(x, gg_fit(x))
plt.xlabel('Position')
plt.ylabel('Flux')

(png, svg, pdf)

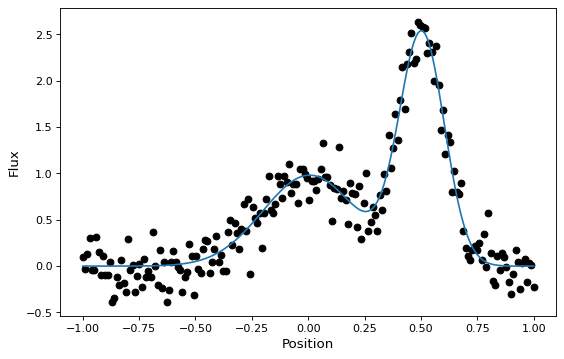
これは、複合モデルを構築するために使用されるすべてのモデルの入出力を正確にマッチングする際にいくつかの複雑さに関連するが、1−Dモデル、2−Dモデル、およびそれらの組み合わせに適用される。あなたはいてもいい組み合わせモデル書類です。

Astropyモデルは関数による畳み込みもサポートしている. convolve_models 複合モデルに戻ります

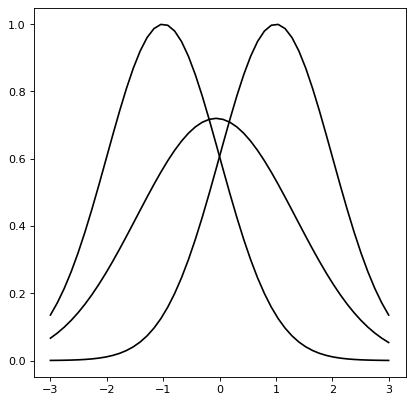
例えば、2つのガウス関数の畳み込みもガウス関数であり、得られる平均(分散)は各ガウスの平均(分散)の和である。

import numpy as np
import matplotlib.pyplot as plt
from astropy.modeling import models
from astropy.convolution import convolve_models

g1 = models.Gaussian1D(1, -1, 1)
g2 = models.Gaussian1D(1, 1, 1)
g3 = convolve_models(g1, g2)

x = np.linspace(-3, 3, 50)
plt.plot(x, g1(x), 'k-')
plt.plot(x, g2(x), 'k-')
plt.plot(x, g3(x), 'k-')

(png, svg, pdf)

全面的な記述¶

いくつかの用語は¶

算術演算子を用いて既存のモデルを組み合わせるだけで新しいモデルを作成することができる. +, -, *, /, and `` **，または使用することで ``|` そして接続(以下説明)と & そして使用することができます fix_inputs() 上の reducing the number of inputs to a model それがそうです。

複合モデル機能を検討する際には、いくつかの混同された用語を明らかにすることが有用である。

用語“モデル”はモデルを指すこともできるし，モデルを指すこともできる クラス モデルでもあります 実例. それがそうです。
- 中のすべてのモデル astropy.modeling それが何かを表しているかどうかにかかわらず function 一種 rotation など，モデルで抽象的に表現されている クラス --具体的には Model --評価モデルのルーチン、必要なパラメータのリスト、およびモデルに関する他のメタデータをカプセル化します。
- 典型的なオブジェクト指向によればモデルは 実例. あるパラメータを持つモデルクラスを呼び出す際に作成されるオブジェクトであるが，多くの場合モデルパラメータの値である.
モデルクラス自体は、ほとんどのモデルが少なくとも1つまたは複数のパラメータを有するので、いくつかの入力データに対してモデルを評価する前に、これらのパラメータを指定しなければならないので、いかなる計算も実行することができない。しかし，モデルクラスの表現からそれに関する情報をいくつか得ることができる.例えば：
```
>>> from astropy.modeling.models import Gaussian1D
>>> Gaussian1D
<class 'astropy.modeling.functional_models.Gaussian1D'>
Name: Gaussian1D
N_inputs: 1
N_outputs: 1
Fittable parameters: ('amplitude', 'mean', 'stddev')
```
そしてモデルを作ることができます 実例. 以下の3つのパラメータの値を入力することで：
```
>>> my_gaussian = Gaussian1D(amplitude=1.0, mean=0, stddev=0.2)
>>> my_gaussian  
<Gaussian1D(amplitude=1.0, mean=0.0, stddev=0.2)>
```
私たちが今持っているのは 実例. の Gaussian1D すべてのパラメータ(原則として適合制約のような他の詳細がある)を充填して、関数であるように計算を実行することができます。
```
>>> my_gaussian(0.2)  
0.6065306597126334
```
多くの場合、本明細書では、クラス/インスタンスの区別がコンテキストとは無関係であるか、またはコンテキストから明確に見える“モデル”のみを言及する。しかし、必要な場合、私たちは区別するつもりだ。
A 複合モデル. Astropyに付随するモデルであってもよい2つ以上の既存のモデルインスタンスを組み合わせることによって作成することができる。 user defined models または他の複合モデルは、1つまたは複数のサポートされた2値演算子からなるPython式を使用する。モデルクラスの組合せは破棄され，4.0版で削除される.
ある場所では用語は 複合モデル. 交換して使用することができる 複合モデル. それがそうです。しかし，本稿では用語を用いた 複合モデル. 引用する. only パイプオペレータを用いて2つ以上のモデルの機能の組み合わせから作成された複合モデルの場合 | 以下に述べる.この区別は本文書ではつねに用いられているが，この違いを理解するのに役立つ可能性がある.

複合モデルを作成する¶

複合モデルを作成する唯一の方法は、Python内の式と二元演算子を使用して既存の単一のモデルおよび/または複合モデルを組み合わせることである。 +, -, *, /, `` **， ``|` そして、 & このうち，いずれも以下の各節で議論する.

警告

V 4.0ではクラスを組み合わせることで複合モデルを作成することを削除した.

2つのモデルを統合した結果は，1つのモデル例である.

>>> two_gaussians = Gaussian1D(1.1, 0.1, 0.2) + Gaussian1D(2.5, 0.5, 0.1)
>>> two_gaussians  
<CompoundModel...(amplitude_0=1.1, mean_0=0.1, stddev_0=0.2, amplitude_1=2.5, mean_1=0.5, stddev_1=0.1)>

この式は、評価に使用可能な新しいモデル例を作成する：

>>> two_gaussians(0.2)  
0.9985190841886609

♪the print 関数は、このオブジェクトに関する詳細な情報を提供する：

>>> print(two_gaussians)
Model: CompoundModel...
Inputs: ('x',)
Outputs: ('y',)
Model set size: 1
Expression: [0] + [1]
Components:
    [0]: <Gaussian1D(amplitude=1.1, mean=0.1, stddev=0.2)>

    [1]: <Gaussian1D(amplitude=2.5, mean=0.5, stddev=0.1)>
Parameters:
    amplitude_0 mean_0 stddev_0 amplitude_1 mean_1 stddev_1
    ----------- ------ -------- ----------- ------ --------
            1.1    0.1      0.2         2.5    0.5      0.1

ここでいくつかの点を指摘する必要がある：このモデルには6つの適切なパラメータがある。節ではさらにパラメータをどのように扱うかを検討する. パラメータそれがそうです。リストがあります 表示法 このような複合モデルを作成するために使用されるものは、本例ではまとめられる。 [0] + [1] それがそうです。♪the [0] そして [1] 以下に列挙するモデルの第1および第2の構成要素を参照してください(本例では、これら2つの構成要素はいずれも Gaussian1D 対象)。

複合モデルの各コンポーネントは単一の非複合モデルである.新しい表現に既存の複合モデルが含まれている場合でも同様である.既存の複合モデルは単一のモデルとはみなされない--逆に，この複合モデルで表される式が拡張される.2つ以上の複合モデルに関する表現は、モデルに関するすべての式の直列である新しい表現を生成する。

>>> four_gaussians = two_gaussians + two_gaussians
>>> print(four_gaussians)
Model: CompoundModel...
Inputs: ('x',)
Outputs: ('y',)
Model set size: 1
Expression: [0] + [1] + [2] + [3]
Components:
    [0]: <Gaussian1D(amplitude=1.1, mean=0.1, stddev=0.2)>

    [1]: <Gaussian1D(amplitude=2.5, mean=0.5, stddev=0.1)>

    [2]: <Gaussian1D(amplitude=1.1, mean=0.1, stddev=0.2)>

    [3]: <Gaussian1D(amplitude=2.5, mean=0.5, stddev=0.1)>
Parameters:
    amplitude_0 mean_0 stddev_0 amplitude_1 ... stddev_2 amplitude_3 mean_3 stddev_3
    ----------- ------ -------- ----------- ... -------- ----------- ------ --------
            1.1    0.1      0.2         2.5 ...      0.2         2.5    0.5      0.1

運営者¶

算術演算子¶

複合モデルは，任意の数の算術演算子を含む式から作成することができる. +, -, *, /, and `` **``Pythonの他の数値オブジェクトの意味と同じ意味です。

注釈

グループ化の場合 / 常に浮動小数点除算である整数除算と // モデルは演算子をサポートしていない).

先の例に示すように，単一の出力を持つモデルに対して，モデルを評価した結果は以下のとおりである. A + B 評価です。 A そして B 与えられた入力をそれぞれ計算し，返す. A そして B それがそうです。これが要求です A そして B 同じ数の入力を受け取り，両者とも1つの出力を持つ.

また，複数の出力を持つモデル間で算術演算子を用いることも可能である.同様に，モデル間の入力数は同じでなければならず，出力数も同じでなければならない.本例では，演算子は要素ごとに演算子に適用され，算術演算子の2つのNumpy配列上での動作方式に類似している.

モデル構図¶

複合モデルを作成するために利用可能な6番目の二元演算子は合成演算子であり，“パイプ”演算子とも呼ばれる. | (Pythonデジタルオブジェクトで実現されているブール“または”演算子と混同しないでください)。合成演算子を用いて作成したモデルは M = F | G 評価する場合は評価と同じです \(g \circ f = g(f(x))\) それがそうです。

注釈

実際には | 演算子は関数複合演算子の意味とは逆である. \(\circ\) 時々迷ってしまいます。これは，Pythonにはこれに対応する演算子記号がないためである.♪the | 演算子は同じように pipe operator UNIXハウジング文法：左オペランドの出力を右オペランドの入力に送ることで，モデルや変換の“パイプ”を形成し，モデルをリンクする.

これは，オペランドの入出力に対する要求が算術演算子とは異なる.合成に対して，すべて必要なのは，左側モデルが右側モデルと同数の出力を持つことである.

簡単な機能モデルの場合、これは、上述した順序付けに関する警告を除いて、機能の組み合わせとまったく同じである。例えば、以下の複合モデルを作成するためには、以下の操作を実行してください。

import numpy as np
import matplotlib.pyplot as plt
from astropy.modeling.models import RedshiftScaleFactor, Gaussian1D

x = np.linspace(0, 1.2, 100)
g0 = RedshiftScaleFactor(0) | Gaussian1D(1, 0.75, 0.1)

plt.figure(figsize=(8, 5))
plt.plot(x, g0(x), 'g--', label='$z=0$')

for z in (0.2, 0.4, 0.6):
    g = RedshiftScaleFactor(z) | Gaussian1D(1, 0.75, 0.1)
    plt.plot(x, g(x), color=plt.cm.OrRd(z),
             label=f'$z={z}$')

plt.xlabel('Energy')
plt.ylabel('Flux')
plt.legend()

(png, svg, pdf)

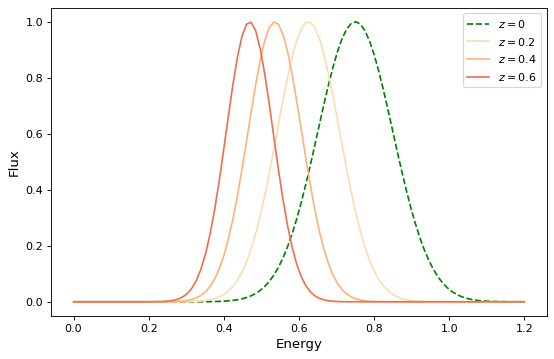
エネルギー空間で赤シフトを実行するのではなく、波長空間で赤シフトを実行したい場合、またフラックスを保存したい場合、ここにはモデルを使用して赤シフトを達成する別の方法がある。 実例. ：

import numpy as np
import matplotlib.pyplot as plt
from astropy.modeling.models import RedshiftScaleFactor, Gaussian1D, Scale

x = np.linspace(1000, 5000, 1000)
g0 = Gaussian1D(1, 2000, 200)  # No redshift is same as redshift with z=0

plt.figure(figsize=(8, 5))
plt.plot(x, g0(x), 'g--', label='$z=0$')

for z in (0.2, 0.4, 0.6):
    rs = RedshiftScaleFactor(z).inverse  # Redshift in wavelength space
    sc = Scale(1. / (1 + z))  # Rescale the flux to conserve energy
    g = rs | g0 | sc
    plt.plot(x, g(x), color=plt.cm.OrRd(z),
             label=f'$z={z}$')

plt.xlabel('Wavelength')
plt.ylabel('Flux')
plt.legend()

(png, svg, pdf)

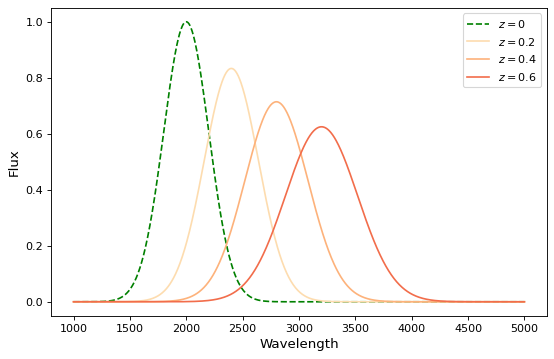
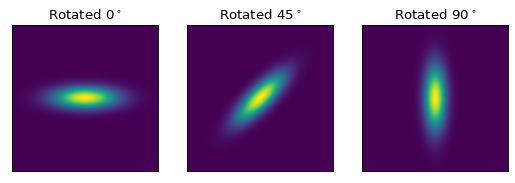
複数の入出力を持つモデルを扱う場合にも，同様の考え方が適用できる.各入力が座標軸とみなされる場合、これは、各軸上の座標のための変換導管を定義する(これらの変換が分離可能であることは必ずしも保証されないが)。例えば：

import numpy as np
import matplotlib.pyplot as plt
from astropy.modeling.models import Rotation2D, Gaussian2D

x, y = np.mgrid[-1:1:0.01, -1:1:0.01]

plt.figure(figsize=(8, 2.5))

for idx, theta in enumerate((0, 45, 90)):
    g = Rotation2D(theta) | Gaussian2D(1, 0, 0, 0.1, 0.3)
    plt.subplot(1, 3, idx + 1)
    plt.imshow(g(x, y), origin='lower')
    plt.xticks([])
    plt.yticks([])
    plt.title(f'Rotated $ {theta}^\circ $')

(png, svg, pdf)

注釈

上の例は少しわざとらしい例です Gaussian2D オプションの回転パラメータがサポートされている。しかし，これは座標回転を任意のモデルにどのように加えるかを示している.

一般に、例えば、2つの出力および1つの入力のみを有する関数を構成することは不可能である：

>>> from astropy.modeling.models import Rotation2D
>>> Rotation2D() | Gaussian1D()  
Traceback (most recent call last):
...
ModelDefinitionError: Unsupported operands for |: Rotation2D (n_inputs=2, n_outputs=2) and Gaussian1D (n_inputs=1, n_outputs=1); n_outputs for the left-hand model must match n_inputs for the right-hand model.

しかし次節でご覧になるように模型直列モデルのいくつかの出力、特に協働して使用する際にのみ変換を適用するモデルを作成する方法を提供する。 mappings それがそうです。

模型直列¶

接続演算子 & また，“接続”と呼ばれることもあり，2つのモデルを1つの完全に分離可能な変換に組み合わせる.すなわち、入力を左側モデルに接続し、右側モデルの入力に接続し、いかなる方法でも混合することなく、2つのモデルの出力によって接続されたタプルを返す新しいモデルを作成する。言い換えると、これは、この2つのモデルを並列に評価するだけであり、モデルタプルに類似したものと見なすことができる。

例えば、2つの座標軸が与えられた場合、2つの座標軸を接続することによって、各座標を異なる因子でスケーリングすることができる。 Scale モデルたち。

>>> from astropy.modeling.models import Scale
>>> separate_scales = Scale(factor=1.2) & Scale(factor=3.4)
>>> separate_scales(1, 2)  
(1.2, 6.8)

また、2つの(または複数の)座標軸上で“1 D”および“2 D”モデルを同時に使用する変換チェーンを構築するために、直列を合成と組み合わせることもできる：

>>> scale_and_rotate = ((Scale(factor=1.2) & Scale(factor=3.4)) |
...                     Rotation2D(90))
>>> scale_and_rotate.n_inputs
2
>>> scale_and_rotate.n_outputs
2
>>> scale_and_rotate(1, 2)  
(-6.8, 1.2)

これはもちろん1つの AffineTransformation2D 適切な変換行列を使用する：

>>> from numpy import allclose
>>> from astropy.modeling.models import AffineTransformation2D
>>> affine = AffineTransformation2D(matrix=[[0, -3.4], [1.2, 0]])
>>> # May be small numerical differences due to different implementations
>>> allclose(scale_and_rotate(1, 2), affine(1, 2))
True

他のテーマ¶

モデル名¶

上述した2つの例において、生成された複合モデルクラスのもう1つの顕著な特徴は、コマンドプロンプトにクラスを印刷する際に表示されるクラス名が“TwoGaussian”、“FourGaussian”などではなく、逆に、各複合モデルが一意のデフォルト名を有するように、“CompoundModel”の直後に実質的に任意の整数からなる生成された名前であることである。これは現在の制限であり、Pythonでは、オブジェクトが式から作成された場合、それが付与される変数の名前(あれば)を“知る”ことを一般的に“知らせる”ことは不可能であるからである。属性は複合モデルインスタンスに直接名前を指定することが可能である. Model.name 属性：：

>>> two_gaussians.name = "TwoGaussians"
>>> print(two_gaussians)  
Model: CompoundModel...
Name: TwoGaussians
Inputs: ('x',)
Outputs: ('y',)
Model set size: 1
Expression: [0] + [1]
Components:
    [0]: <Gaussian1D(amplitude=1.1, mean=0.1, stddev=0.2)>

    [1]: <Gaussian1D(amplitude=2.5, mean=0.5, stddev=0.1)>
Parameters:
    amplitude_0 mean_0 stddev_0 amplitude_1 mean_1 stddev_1
    ----------- ------ -------- ----------- ------ --------
            1.1    0.1      0.2         2.5    0.5      0.1

索引とスライス¶

本明細書の前のいくつかの例に示すように、複合モデルを作成する際に、モデルの各構成要素には、ゼロから始まる整数インデックスが割り当てられる。操作順序にかかわらず，モデルを定義する式を左から右へ読み込むだけで，これらのインデックスを割り当てることができる.例えば：

>>> from astropy.modeling.models import Const1D
>>> A = Const1D(1.1, name='A')
>>> B = Const1D(2.1, name='B')
>>> C = Const1D(3.1, name='C')
>>> M = A + B * C
>>> print(M)
Model: CompoundModel...
Inputs: ('x',)
Outputs: ('y',)
Model set size: 1
Expression: [0] + [1] * [2]
Components:
    [0]: <Const1D(amplitude=1.1, name='A')>

    [1]: <Const1D(amplitude=2.1, name='B')>

    [2]: <Const1D(amplitude=3.1, name='C')>
Parameters:
    amplitude_0 amplitude_1 amplitude_2
    ----------- ----------- -----------
            1.1         2.1         3.1

In this example the expression is evaluated (B * C) + A--that is, the multiplication is evaluated before the addition per usual arithmetic rules. However, the components of this model are simply read off left to right from the expression A + B * C, with A -> 0, B -> 1, C -> 2. If we had instead defined M = C * B + A then the indices would be reversed (though the expression is mathematically equivalent). This convention is chosen for simplicity--given the list of components it is not necessary to jump around when mentally mapping them to the expression.

複合モデルの個々のコンポーネントを抽出することができます M これにインデックス記号を用いることで.次は上の例です M[1] モデルを返却すべきだ B **

>>> M[1]
<Const1D(amplitude=2.1, name='B')>

一つ持ってもいいです スライス.スライス 複合モデルの。これは新しい複合モデルに戻ります サブ表現. スライス選択のモデルについて触れた。これは分割に従っています list Pythonの配列です始点は含まれており，終点は排除されている.このような一面は M[1:3] (または単に M[1:] )モデルの選択 B そして C (そしてすべて オペレータ. 彼らの間)。したがって，結果モデルは部分式のみを計算する. B * C **

>>> print(M[1:])
Model: CompoundModel
Inputs: ('x',)
Outputs: ('y',)
Model set size: 1
Expression: [0] * [1]
Components:
    [0]: <Const1D(amplitude=2.1, name='B')>

    [1]: <Const1D(amplitude=3.1, name='C')>
Parameters:
    amplitude_0 amplitude_1
    ----------- -----------
            2.1         3.1

注釈

スライスのパラメータ名は4.0以前のバージョンとは異なる.従来，パラメータ名はスライスするモデルの名前と同じであった.現在，スライスされたモデルを除いて，これらはこのようなタイプの複合モデルに必要である.すなわち，スライスモデルはつねにそのコンポーネントの相対インデックスで始まるため，パラメータ名は0接尾辞で始まる.

注釈

4.0からスライスの振舞いは従来よりも厳しい.例えば、もし：

m = m1 * m2 + m3

1つのスライスを使って m[1:3] これは以前モデルに戻ります m2 + m3 Mがこのようなサブモデルを持っていなくても.4.0からスライスは1つのサブモデルに対応しなければならない(複合モデルを計算する計算リンクの中間結果に対応する).そのため：

m1 * m2

サブモデル(すなわち``M) [:2] )でも ``m[1:3] 違います。現在、これは、以下のように、より簡単な表現であることを意味する。

m = m1 + m2 + m3 + m4

すべてのサブモジュールの一部であるので、どのスライスも原則的に有効でなければならない場合、M 1を含むスライスのみが有効である(評価の順序は：

((m1 + m2) + m3) + m4

サブモデルが利用可能であることを望む複合モデルを作成する任意の人が、丸括弧を明示的に使用するか、または後続式で使用される中間モデルを定義して、それらをコンテキストに従ってスライスまたは単純なインデックスを使用して抽出することができるように提案する。例えば、作るためには m2 + m3 スライスでアクセスを定義することができる m AS：：

m = m1 + (m2 + m3) + m4. In this case ``m[1:3]`` will work.

部分式の新しい複合モデルは、任意の他のモデルのように値を求めることができる：

>>> M[1:](0)  
6.51

Although the model M was composed entirely of Const1D models in this example, it was useful to give each component a unique name (A, B, C) in order to differentiate between them. This can also be used for indexing and slicing:

>>> print(M['B'])
Model: Const1D
Name: B
Inputs: ('x',)
Outputs: ('y',)
Model set size: 1
Parameters:
    amplitude
    ---------
          2.1

このような場合には M['B'] 相等しい. M[1] それがそうです。しかし，名前を用いることにより，そのコンポーネントがどのインデックスにあるかを心配する必要はない(これは，複数の複合モデルを組み合わせる際に特に有用になる).しかしながら、現在の制限は、複合モデルの各コンポーネントが一意の名前を有していなければならないことであり、いくつかのコンポーネントが重複する名前を有する場合、それらはそれらの整数索を介してアクセスすることしかできないことである。

スライスは名前にも適用される.名前を用いた場合，始点と終点は どちらも含まれている **

>>> print(M['B':'C'])
Model: CompoundModel...
Inputs: ('x',)
Outputs: ('y',)
Model set size: 1
Expression: [0] * [1]
Components:
    [0]: <Const1D(amplitude=2.1, name='B')>

    [1]: <Const1D(amplitude=3.1, name='C')>
Parameters:
    amplitude_0 amplitude_1
    ----------- -----------
            2.1         3.1

だからこの場合は M['B':'C'] 相等しい. M[1:3] それがそうです。

パラメータ¶

複合モデルに初めて遭遇した場合，すべてのパラメータをどのように正確に扱うかという問題がしばしば生じる.私たちはこれまでいくつかのヒントを与える例を見てきたが、より詳細な説明が必要だ。これはまた改善可能な最大の分野の一つである-現在の行動は実用的でなければならないが、理想的ではない。(いくつかの可能な改善は、パラメータを再命名することができ、複合モデルにおけるパラメータ数を縮小する方法を提供することを含む。

モデルの一般文書で述べたように parameters それぞれのモデルには param_names これは、すべてのモデルの調整可能なパラメータのタプルを含む。これらの名前は規範的な順序で与えられており，この順序もインスタンス化モデルの際に指定すべきパラメータの順序に対応している.

複合モデルにおいて現在命名パラメータに用いられている簡単な提案は以下のとおりである. param_names 上記の部分で説明したように、各コンポーネントモデルにおけるデータは、左から右の順に接続されている索引とスライスそれがそうです。ただし，パラメータ名ごとに付加されている. _<#> どこですか <#> パラメータが属するコンポーネントモデルのインデックスである.例えば：

>>> Gaussian1D.param_names
('amplitude', 'mean', 'stddev')
>>> (Gaussian1D() + Gaussian1D()).param_names
('amplitude_0', 'mean_0', 'stddev_0', 'amplitude_1', 'mean_1', 'stddev_1')

一貫性を保つために、すべてのコンポーネントが重複したパラメータ名を持っているわけではなくても、このスキームに従う。

>>> from astropy.modeling.models import RedshiftScaleFactor
>>> (RedshiftScaleFactor() | (Gaussian1D() + Gaussian1D())).param_names
('z_0', 'amplitude_1', 'mean_1', 'stddev_1', 'amplitude_2', 'mean_2',
'stddev_2')

ある程度，複合モデルがそのパラメータのインタフェースにおいて他のモデルと一定の整合性を保つためには，このような方式が必要である.しかし、一人で道に迷った場合は、ご利用いただけます indexing 事を容易にする。複合モデルから単一のコンポーネントが返されると、コンポーネントに関連するパラメータは、その元の名前でアクセスすることができるが、複合モデルに再結合される：

>>> a = Gaussian1D(1, 0, 0.2, name='A')
>>> b = Gaussian1D(2.5, 0.5, 0.1, name='B')
>>> m = a + b
>>> m.amplitude_0
Parameter('amplitude', value=1.0)

これは以下のようなものです

>>> m['A'].amplitude
Parameter('amplitude', value=1.0)

この2つを同じパラメータの異なる“ビュー”と見なすことができます。更新のうちの1つはもう1つを更新します：

>>> m.amplitude_0 = 42
>>> m['A'].amplitude
Parameter('amplitude', value=42.0)
>>> m['A'].amplitude = 99
>>> m.amplitude_0
Parameter('amplitude', value=99.0)

しかし原始的な Gaussian1D 実例. a 更新されました：

>>> a.amplitude
Parameter('amplitude', value=99.0)

これは，4.0までのバージョンでの振舞いとは異なる.いま，複合モデルパラメータはオリジナルモデルと同じParameterインスタンスを共有する.

高度なマッピング¶

先のいくつかの例では、モデルを使用してモデルをリンクして変換された“パイプ”を形成する方法が見られました composition そして concatenation それがそうです。より複雑な変換チェーン(例えば、WCS変換)の作成を支援するために、新しい“Mapping”モデルクラスが提供される。

Mapping models do not (currently) take any parameters, nor do they perform any numeric operation. They are for use solely with the concatenation (&) and composition (|) operators, and can be used to control how the inputs and outputs of models are ordered, and how outputs from one model are mapped to inputs of another model in a composition.

現在2つのマッピングモデルしかありません Identity (汎化された名前もある) Mapping それがそうです。

♪the Identity マッピングは、そのままではなく、1つまたは複数の入力を渡すだけである。これは、それが受け入れる入出力数を指定する整数でインスタンス化されなければならない。これは，モデルが受け取る入力数に応じてモデルの“次元”をわずかに拡張するために用いることができる.ここでは concatenation 次の例を見ました

>>> m = (Scale(1.2) & Scale(3.4)) | Rotation2D(90)

2つの座標入力は個別にスケーリングされ、互いに回転する。ただし，座標の1つだけをスケーリングしたいと仮定する.簡単に使えばいいです。 Scale(1) その中の一つ、あるいは他のどんなことも実際には実行できないモデルだ。しかし，これは不必要な計算オーバヘッドも増加するため，座標がスケーリングや変換されないことを簡単に指定してもよい.これはとても良い使用例です Identity ：

>>> from astropy.modeling.models import Identity
>>> m = Scale(1.2) & Identity(1)
>>> m(1, 2)  
(1.2, 2.0)

これは、第1の入力をスケーリングし、第2の入力をそのまま渡す。これを用いて多軸WCS変換においてより複雑なステップを確立することができる.例えば3つの軸があって最初の軸だけをズームしたい場合

>>> m = Scale(1.2) & Identity(2)
>>> m(1, 2, 3)  
(1.2, 2.0, 3.0)

(もちろん最後の例も書くことができます Scale(1.2) & Identity(1) & Identity(1) ()

♪the Mapping モデルの類似点は，入力を何も修正しないことである.しかし，入力のコピー，並べ替え，さらには直接破棄を可能にするため，より汎用的である.これは単一のパラメータを使用してインスタンス化される：a tuple その項数は Mapping 生まれるはずです。1タプルは入ることを意味します Mapping 1つだけ出力されます2タプル以上のタプルについては、以下同様である(タプルの長さは入力の数よりも大きくはならないが、値は空では得られない)。このマッピングの要素は、入力されたインデックスに対応する整数である。例えば、マッピングは Mapping((0,)) 相等しい. Identity(1) --最初(0番目)の入力のみを受けて返します。

>>> from astropy.modeling.models import Mapping
>>> m = Mapping((0,))
>>> m(1.0)
1.0

同じように Mapping((0, 1)) 相等しい. Identity(2) ちょっと待って。しかし、 Mapping 出力の任意の並べ替えも許可されています：

>>> m = Mapping((1, 0))
>>> m(1.0, 2.0)
(2.0, 1.0)

>>> m = Mapping((1, 0, 2))
>>> m(1.0, 2.0, 3.0)
(2.0, 1.0, 3.0)

出力は廃棄される可能性もあります

>>> m = Mapping((1,))
>>> m(1.0, 2.0)
2.0

>>> m = Mapping((0, 2))
>>> m(1.0, 2.0, 3.0)
(1.0, 3.0)

複製されています

>>> m = Mapping((0, 0))
>>> m(1.0)
(1.0, 1.0)

>>> m = Mapping((0, 1, 1, 2))
>>> m(1.0, 2.0, 3.0)
(1.0, 2.0, 2.0, 3.0)

3つの座標軸上で複数の変換(分離可能である場合もあれば、そうでないものもある)を実行する複雑な例は、以下のようになることができる。

>>> from astropy.modeling.models import Polynomial1D as Poly1D
>>> from astropy.modeling.models import Polynomial2D as Poly2D
>>> m = ((Poly1D(3, c0=1, c3=1) & Identity(1) & Poly1D(2, c2=1)) |
...      Mapping((0, 2, 1)) |
...      (Poly2D(4, c0_0=1, c1_1=1, c2_2=2) & Gaussian1D(1, 0, 4)))
...
>>> m(2, 3, 4)  
(41617.0, 0.7548396019890073)

This expression takes three inputs: \(x\), \(y\), and \(z\). It first takes \(x \rightarrow x^3 + 1\) and \(z \rightarrow z^2\). Then it remaps the axes so that \(x\) and \(z\) are passed in to the Polynomial2D to evaluate \(2x^2z^2 + xz + 1\), while simultaneously evaluating a Gaussian on \(y\). The end result is a reduction down to two coordinates. You can confirm for yourself that the result is correct.

これは本質的に任意の複雑な変換図の可能性を開いている.これらのマッピングを容易にナビゲーションおよび推論することができる高度に複雑な複合モデルは現在のところないが、これは将来のバージョンで強化される可能性がある。

モデル降階¶

In order to save much duplication in the construction of complex models, it is possible to define one complex model that covers all cases where the variables that distinguish the models are made part of the model's input variables. The fix_inputs function allows defining models derived from the more complex one by setting one or more of the inputs to a constant value. Examples of this sort of situation arise when working out the transformations from detector pixel to RA, Dec, and lambda for spectrographs when the slit locations may be moved (e.g., fiber fed or commandable slit masks), or different orders may be selected (e.g., Eschelle). In the case of order, one may have a function of pixel x, y, spectral_order that map into RA, Dec and lambda. Without specifying spectral_order, it is ambiguous what RA, Dec and Lambda corresponds to a pixel location. It is usually possible to define a function of all three inputs. Presuming this model is general_transform then fix_inputs may be used to define the transform for a specific order as follows:

**

>>> order1_transform = fix_inputs(general_transform, {'order': 1})  

creates a new compound model that takes only pixel position and generates RA, Dec, and lambda. The fix_inputs function can be used to set input values by position (0 is the first) or by input variable name, and more than one can be set in the dictionary supplied.

入力モデルが境界枠を持つ場合，生成されたモデルは入力座標の境界を削除する.

サブモデルを交換する.¶

replace_submodel() 一致した名前を有するサブモデルを別のサブモデルに置き換えることによって、新しいモデルを作成する。新しいサブモデルと旧モデルの入出力数は一致すべきである.**

>>> from astropy.modeling import models
>>> shift = models.Shift(-1) & models.Shift(-1)
>>> scale = models.Scale(2) & models.Scale(3)
>>> scale.name = "Scale"
>>> model = shift | scale
>>> model(2, 1)  
(2.0, 0.0)
>>> new_model = model.replace_submodel('Scale', models.Rotation2D(90, name='Rotation'))
>>> new_model(2, 1)  
(6.12e-17, 1.0)