新しいモデルクラスを定義する

本稿では、モデルをパッケージに追加したり、カスタムモデルを作成したりする方法を紹介します。簡単に言うと，すべてのモデルパラメータを定義し，モデルを評価する関数，すなわちモデルを実現する数学関数を計算する必要がある.モデルが適合可能である場合，線形適合アルゴリズムを用いるためには，パラメータに関する微分係数の関数を計算する必要があり，非線形フィッティングを用いる場合にはオプションの関数が必要となる。

基本カスタマイズモデル

ほとんどの場合 custom_model 装飾者は新しいものを作るための簡単な方法を提供します Model 既存のPythonからオブジェクトの初期化を呼び出すことができます。以下の例では、2つのガウスモデルからなるモデルを設定する方法を示す。

import numpy as np
import matplotlib.pyplot as plt
from astropy.modeling.models import custom_model
from astropy.modeling.fitting import LevMarLSQFitter

# Define model
@custom_model
def sum_of_gaussians(x, amplitude1=1., mean1=-1., sigma1=1.,
                        amplitude2=1., mean2=1., sigma2=1.):
    return (amplitude1 * np.exp(-0.5 * ((x - mean1) / sigma1)**2) +
            amplitude2 * np.exp(-0.5 * ((x - mean2) / sigma2)**2))

# Generate fake data
np.random.seed(0)
x = np.linspace(-5., 5., 200)
m_ref = sum_of_gaussians(amplitude1=2., mean1=-0.5, sigma1=0.4,
                         amplitude2=0.5, mean2=2., sigma2=1.0)
y = m_ref(x) + np.random.normal(0., 0.1, x.shape)

# Fit model to data
m_init = sum_of_gaussians()
fit = LevMarLSQFitter()
m = fit(m_init, x, y)

# Plot the data and the best fit
plt.plot(x, y, 'o', color='k')
plt.plot(x, m(x))

(png, svg, pdf)

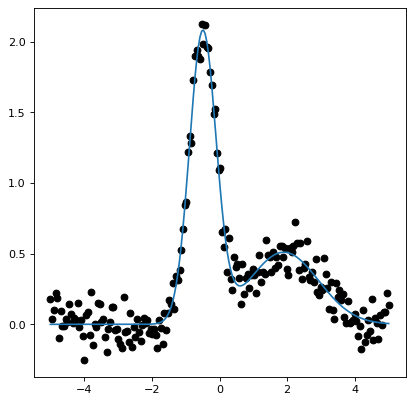
この修飾器はモデルを設定することもサポートしています fit_deriv 複数の入力を持つモデルを作成する.通常の出荷機能としても使用することができます(例えば SumOfGaussians = custom_model(sum_of_gaussians) )ではなく、装飾師としてである。ご参照ください custom_model より多くの例の文書については、参照されたい。

一次元ガウスモデルの逐次定義

中に記載された例 Basic custom models 多くの簡単な場合に利用可能であるが，次節ではモデルクラスをどのように構築するかを述べる.完全なモデルクラスを定義することは、例えば、より専用のパラメータを提供するために、または実質的にサポートされていない特別な機能を実現するために必要である可能性がある custom_model 工場機能。

以下，一次元ガウスモデルを例に詳細に説明する.モデルには2つの基底類がある.もしモデルが適切であれば、それは継承すべきです FittableModel そうでなければサブクラスであるべきである Model それがそうです。

モデルがパラメータを用いる場合は，モデルのクラス定義に用いるべきである. Parameter 記述子。Parameter構造関数のすべてのパラメータは任意であり、パラメータのデフォルト値、パラメータのテキスト説明(適用可能)を含むことができる。 help 文書生成)，およびパラメータ値のデフォルト制約とカスタムgetter/setter.また、カスタムコードがモデル定義に従ってパラメータ値が有効であるかどうか(例えば、非負の値でなければならないかどうか)を検査することができるように、各パラメータについて1つの“ベリファイア”方法を定義することができる。中の例を参照されたい Parameter.validator もっと細かいことを知っています。

from astropy.modeling import Fittable1DModel, Parameter

class Gaussian1D(Fittable1DModel):
    n_inputs = 1
    n_outputs = 1

    amplitude = Parameter()
    mean = Parameter()
    stddev = Parameter()

♪the n_inputs そして n_outputs クラス属性は整数でなければならず，モデルを評価するために入力される引数の数とその返す出力数を示す.入力と出力のラベルは inputs そして outputs ，自動生成される.デフォルト値は、クラスに必要な値を割り当てることでカバーすることができます __init__ メソッド、呼び出しています super それがそうです。 outputs そして inputs 長さの文字列のタプルでなければなりません n_outputs そして n_inputs それぞれです。出力は、入力と同じラベルを有する場合がある(例えば、 inputs = ('x', 'y') そして outputs = ('x', 'y') )である。しかしながら、入力は互いに衝突することはできない(例えば、 inputs = ('x', 'x') 正しくない)，出力についても同様である.

There are two helpful base classes in the modeling package that can be used to avoid specifying n_inputs and n_outputs for most common models. These are Fittable1DModel and Fittable2DModel. For example, the actual Gaussian1D model is a subclass of Fittable1DModel. This helps cut down on boilerplate by not having to specify n_inputs, n_outputs, inputs and outputs for many models (follow the link to Gaussian1D to see its source code, for example).

回帰的には、適合可能なモデルは線形であってもよいし、非線形であってもよい。属性のデフォルト値 linear 属性は False それがそうです。線形モデルは定義すべきです linear 類属性は True それがそうです。このモデルは非線形であるため，デフォルト値を用いることができる.

自己を継承する. Fittable1DModel Vbl.ある Model._separable 属性は設定されています True それがそうです。他のすべてのモデルはこの属性を定義して指示すべきである モデル分離性 それがそうです。

次に名前を提供します evaluate このモデルを評価し fit_deriv パラメータに対する微分係数を計算する.これらは正常な方法かもしれません classmethod あるいは、あるいは staticmethod 約束したにもかかわらず staticmethod 関数がオブジェクトの他の属性に依存しない場合(すなわち、参照しない self )やクラスの他の属性、例えば classmethod それがそうです。求め方は，すべての入力座標を単独のパラメータとし，すべてのモデルパラメータのリスト順序が同じである. param_names それがそうです。

この例の場合：

@staticmethod
def evaluate(x, amplitude, mean, stddev):
    return amplitude * np.exp((-(1 / (2. * stddev**2)) * (x - mean)**2))

明確にすべきは evaluate 手法は，モデルのパラメータ値をパラメータとするように設計しなければならない.これは、パラメータ値がモデルの属性を通過しているように見える(例えば、 model.amplitude )である。ただし，パラメータ値を直接渡す. evaluate 多くの場合、それを使用するより効果的な方法、例えばアクセサリである。

あなたのモデルのユーザーは通常使用しません evaluate 直接行きましょう。代わりに、彼らはモデルの一例を作成し、いくつかの入力でそれをアップグレードする。♪the __call__ モデル使用方法 evaluate 内部では，ユーザはこれを意識する必要はない.デフォルト設定 __call__ モデルの評価を試みる前に、実装は、入力されたフォーマットが正しいかどうか、Numpyのブロードキャストルールに従うかどうかをチェックするなど、いくつかの詳細を扱う。

像 evaluate vt.的 fit_deriv 方法すべての座標とすべてのパラメータ値をパラメータとして入力とする.非線形モデルを計算する数値微分係数を選択することができる場合 fit_deriv 方法はすべきである. None **

@staticmethod
def fit_deriv(x, amplitude, mean, stddev):
    d_amplitude = np.exp(- 0.5 / stddev**2 * (x - mean)**2)
    d_mean = (amplitude *
              np.exp(- 0.5 / stddev**2 * (x - mean)**2) *
              (x - mean) / stddev**2)
    d_stddev = (2 * amplitude *
                np.exp(- 0.5 / stddev**2 * (x - mean)**2) *
                (x - mean)**2 / stddev**3)
    return [d_amplitude, d_mean, d_stddev]

私たちは確かにやったことに注意してください not 定義しなければなりません __init__ 方法や1つ __call__ 手法は我々のモデルに用いた.ほとんどのモデルでは __init__ 同じパターンに従い，パラメータ値を位置パラメータとし，いくつかの選択可能なキーワードパラメータ(制約など)を後にする.モデリングフレームワーク自動生成 __init__ 正しい呼び出しを持つ署名を持つクラス(呼び出しにより) help(Gaussian1D.__init__) 先ほど定義したモデル例では).

場合によってはカスタムを定義する必要があるかもしれません __init__ それがそうです。例えば Gaussian2D model takes an optional cov_matrix argument which can be used as an alternative way to specify the x/y_stddev and theta parameters. This is perfectly valid so long as the _ _init__ﾟ`実際のパラメータのために適切な値を決定し、スーパーを呼び出します。 ``__init__ 標準的な論拠を用いる。概略的には、以下のように見える。

def __init__(self, amplitude, x_mean, y_mean, x_stddev=None,
             y_stddev=None, theta=None, cov_matrix=None, **kwargs):
    # The **kwargs here should be understood as other keyword arguments
    # accepted by the basic Model.__init__ (such as constraints)
    if cov_matrix is not None:
        # Set x/y_stddev and theta from the covariance matrix
        x_stddev = ...
        y_stddev = ...
        theta = ...

    # Don't pass on cov_matrix since it doesn't mean anything to the base
    # class
    super().__init__(amplitude, x_mean, y_mean, x_stddev, y_stddev, theta,
                     **kwargs)

完全な例

import numpy as np
from astropy.modeling import Fittable1DModel, Parameter

class Gaussian1D(Fittable1DModel):
    amplitude = Parameter()
    mean = Parameter()
    stddev = Parameter()

    @staticmethod
    def evaluate(x, amplitude, mean, stddev):
        return amplitude * np.exp((-(1 / (2. * stddev**2)) * (x - mean)**2))

    @staticmethod
    def fit_deriv(x, amplitude, mean, stddev):
        d_amplitude = np.exp((-(1 / (stddev**2)) * (x - mean)**2))
        d_mean = (2 * amplitude *
                  np.exp((-(1 / (stddev**2)) * (x - mean)**2)) *
                  (x - mean) / (stddev**2))
        d_stddev = (2 * amplitude *
                    np.exp((-(1 / (stddev**2)) * (x - mean)**2)) *
                    ((x - mean)**2) / (stddev**3))
        return [d_amplitude, d_mean, d_stddev]

線形モデルの完全な例

この例は、モデルクラスの別のオプション機能、すなわち 逆に. それがそうです。一個 inverse 実現は…。 property これは、逆を有するいくつかのモデルインスタンスについて、そのモデルの逆を計算する新しいモデルインスタンス(必ずしも逆されているモデルと同じクラスを有する必要はない)に戻る。 model.inverse(model(*input)) == input それがそうです。

import numpy as np
from astropy.modeling import Fittable1DModel, Parameter

class LineModel(Fittable1DModel):
    slope = Parameter()
    intercept = Parameter()
    linear = True

    @staticmethod
    def evaluate(x, slope, intercept):
        return slope * x + intercept

    @staticmethod
    def fit_deriv(x, slope, intercept):
        d_slope = x
        d_intercept = np.ones_like(x)
        return [d_slope, d_intercept]

    @property
    def inverse(self):
        new_slope = self.slope ** -1
        new_intercept = -self.intercept / self.slope
        return LineModel(slope=new_slope, intercept=new_intercept)

注釈

上の例は内蔵のものとほぼ同じです Linear1D モデルです。