ヒストグラムボックスを選択する¶
♪the astropy.visualization モジュールは hist() 関数は,matplotlibヒストグラム関数の拡張であり,ヒストグラムをより柔軟に指定することを許す.図面を持たない計算箱に関する情報は、参照されたい astropy.stats.histogram() それがそうです。
同じ5000点の下位集合から構成される2つのヒストグラムを考慮すると、1つ目はmatplotlibのデフォルト値10個のヒストグラムを使用し、2つ目は任意に選択された200個のヒストグラムを使用する。
import numpy as np
import matplotlib.pyplot as plt
# generate some complicated data
rng = np.random.RandomState(0)
t = np.concatenate([-5 + 1.8 * rng.standard_cauchy(500),
-4 + 0.8 * rng.standard_cauchy(2000),
-1 + 0.3 * rng.standard_cauchy(500),
2 + 0.8 * rng.standard_cauchy(1000),
4 + 1.5 * rng.standard_cauchy(1000)])
# truncate to a reasonable range
t = t[(t > -15) & (t < 15)]
# draw histograms with two different bin widths
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
fig.subplots_adjust(left=0.1, right=0.95, bottom=0.15)
for i, bins in enumerate([10, 200]):
ax[i].hist(t, bins=bins, histtype='stepfilled', alpha=0.2, density=True)
ax[i].set_xlabel('t')
ax[i].set_ylabel('P(t)')
ax[i].set_title(f'plt.hist(t, bins={bins})',
fontdict=dict(family='monospace'))
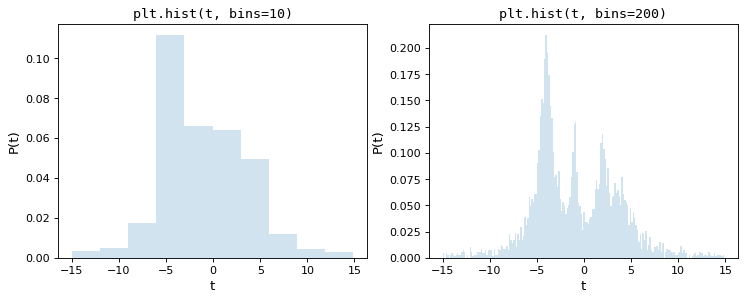
目視により,これらの選択のいずれも最適であり,10ボックスに対してはデータ分布の微細構造が失われ,200ボックスでは単一ボックスの高さがサンプリング誤差の影響を受けることが明らかになった.多くの科学者が採用している何度も試してみる方法は反復的な方法であり、この両者の間に適切な中点を見つけることを試みている。
Astropy‘s hist() 関数はヒストグラムのカラムサイズを自動的に調整するいくつかの方法を提供することでこの問題を解決する.その文法はmatplotlibの文法と同じである plt.hist 関数ですが bins ビットを自動的に選択するための4つの異なる方法のうちの1つを指定することを可能にするパラメータ。これらの方法は astropy.stats.histogram() その文法は np.histogram 機能します。
正常参考規則¶
カラムの数を調整する最も簡単な方法はScottの通常の引用規則に基づく(ここで実現される) scott_bin_width() )およびFreedman&Diaconis(実装 freedman_bin_width() )である。これらのルールは,データが正規分布に近いと仮定し,ヒストグラムと基本データ分布の違いを最小化するための経験則を適用することで行われる.
次の図に上記データセット上のこの2つのルールの結果を示す.
import numpy as np
import matplotlib.pyplot as plt
from astropy.visualization import hist
# generate some complicated data
rng = np.random.RandomState(0)
t = np.concatenate([-5 + 1.8 * rng.standard_cauchy(500),
-4 + 0.8 * rng.standard_cauchy(2000),
-1 + 0.3 * rng.standard_cauchy(500),
2 + 0.8 * rng.standard_cauchy(1000),
4 + 1.5 * rng.standard_cauchy(1000)])
# truncate to a reasonable range
t = t[(t > -15) & (t < 15)]
# draw histograms with two different bin widths
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
fig.subplots_adjust(left=0.1, right=0.95, bottom=0.15)
for i, bins in enumerate(['scott', 'freedman']):
hist(t, bins=bins, ax=ax[i], histtype='stepfilled',
alpha=0.2, density=True)
ax[i].set_xlabel('t')
ax[i].set_ylabel('P(t)')
ax[i].set_title(f'hist(t, bins="{bins}")',
fontdict=dict(family='monospace'))
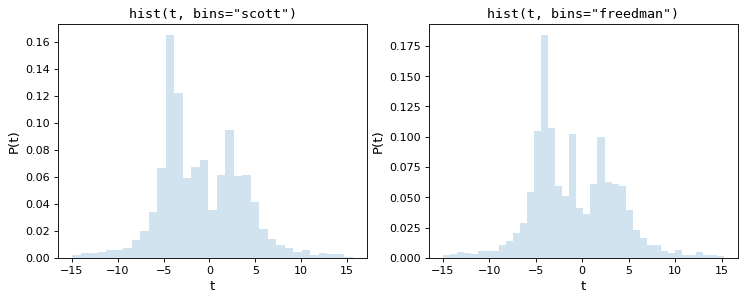
私たちが見ているように、この2つの経験則は、データ表現とノイズ抑制との間に良好なトレードオフを提供する中間数のボックスを選択している。
ベイズモデル¶
スコット規則やフリードマン-ディアコーニス規則のような経験則は迅速で便利であるが,それらのデータに対する強い仮定は,より複雑な分布にとって最適ではない.倉位選択の他の方法は,実データに基づいて計算された適応度関数を用いて最適な倉位を選択する.Astropyはその2つの例を実現している:Knuthルール(ここで knuth_bin_width() )とベイジアンブロック(では bayesian_blocks() )。
Knuthルールは,ヒストグラムのデータに対する近似誤差を最小化するために一定のビンサイズを選択するが,ベイジアンブロックはより柔軟な方法を用いてビン幅を変更することを許す.両手法ともデータセット全体のコスト関数を最小化する必要があるため,上記の経験則よりも計算的に密集している.以下に上記データセットのこれらの過程の結果を示す.
import warnings
import numpy as np
import matplotlib.pyplot as plt
from astropy.visualization import hist
# generate some complicated data
rng = np.random.RandomState(0)
t = np.concatenate([-5 + 1.8 * rng.standard_cauchy(500),
-4 + 0.8 * rng.standard_cauchy(2000),
-1 + 0.3 * rng.standard_cauchy(500),
2 + 0.8 * rng.standard_cauchy(1000),
4 + 1.5 * rng.standard_cauchy(1000)])
# truncate to a reasonable range
t = t[(t > -15) & (t < 15)]
# draw histograms with two different bin widths
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
fig.subplots_adjust(left=0.1, right=0.95, bottom=0.15)
for i, bins in enumerate(['knuth', 'blocks']):
hist(t, bins=bins, ax=ax[i], histtype='stepfilled',
alpha=0.2, density=True)
ax[i].set_xlabel('t')
ax[i].set_ylabel('P(t)')
ax[i].set_title(f'hist(t, bins="{bins}")',
fontdict=dict(family='monospace'))
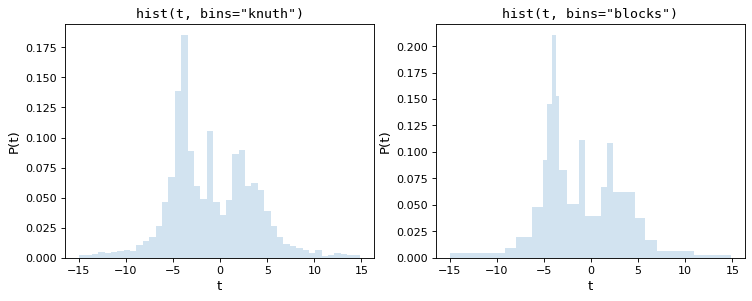
この2つのパラメータは分布の形状を非常に正確に捉えており bins='blocks' パネル選択ボックス幅は,データ中のローカル構造によってボックス幅が異なる.これらのベイズ最適化方法は、標準デフォルト値と比較して、ヒストグラム入庫を選択するためのより原則的な方法を提供する。