畳み込み核¶
序言と概念¶
畳み込みモジュールは、天文学で最も一般的なアプリケーションをカバーするために、いくつかの内蔵カーネルを提供する。特定のアプリケーションに適合するために、配列からカスタムカーネルを定義するか、または既存のカーネルを組み合わせてもよい。
各フィルタコアは、その応答関数によって特徴付けられる。時系列に対しては“インパルス応答関数”,画像に対しては“点拡張関数”と呼ぶ.各カーネルについて,この応答関数は FittableModel グリッド上で使用しています discretize_model() 入庫データとの離散畳み込みに利用可能なカーネル配列を得る.
実例.¶
1次元カーネル.¶
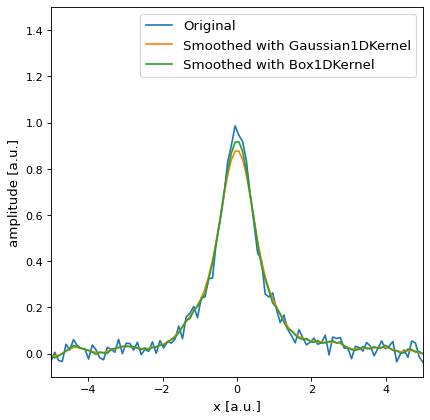
フィルタリングの1つのアプリケーションは、ノイズのあるデータを平滑化することである。この例では騒々しいローレンツ曲線を考えてみましょう
>>> import numpy as np
>>> from astropy.modeling.models import Lorentz1D
>>> from astropy.convolution import convolve, Gaussian1DKernel, Box1DKernel
>>> lorentz = Lorentz1D(1, 0, 1)
>>> x = np.linspace(-5, 5, 100)
>>> data_1D = lorentz(x) + 0.1 * (np.random.rand(100) - 0.5)
ノイズのあるデータを平滑化する Gaussian1DKernel 標準偏差は2画素:
>>> gauss_kernel = Gaussian1DKernel(2)
>>> smoothed_data_gauss = convolve(data_1D, gauss_kernel)
同じデータを平滑化する Box1DKernel 幅5画素:
>>> box_kernel = Box1DKernel(5)
>>> smoothed_data_box = convolve(data_1D, box_kernel)
以下の図は結果を説明する。
他には astropy 畳み込み関数 convolve そして convolve_fft カーネルと numpy あるいは…。 scipy このようにして array 属性です。ほとんどの場合これは astropy 畳み込みは,データ中にNaN値が存在すると正常に動作しない.
>>> smoothed = np.convolve(data_1D, box_kernel.array)
2 Dコア¶
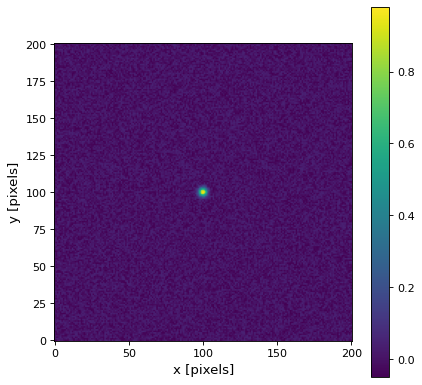
すべての2 Dコアは対称であるため,1方向の幅を指定すれば十分である.したがって,2 Dカーネルの使用は基本的に1 Dカーネルと同様である.ここでは,画像中に振幅1のガウス形状の小さい信号源を持ち,10%のノイズを付加することを考える.
>>> import numpy as np
>>> from astropy.convolution import convolve, Gaussian2DKernel, Tophat2DKernel
>>> from astropy.modeling.models import Gaussian2D
>>> gauss = Gaussian2D(1, 0, 0, 3, 3)
>>> # Fake image data including noise
>>> x = np.arange(-100, 101)
>>> y = np.arange(-100, 101)
>>> x, y = np.meshgrid(x, y)
>>> data_2D = gauss(x, y) + 0.1 * (np.random.rand(201, 201) - 0.5)
ノイズのあるデータを平滑化する Gaussian2DKernel 標準偏差は2画素:
>>> gauss_kernel = Gaussian2DKernel(2)
>>> smoothed_data_gauss = convolve(data_2D, gauss_kernel)
ノイズのあるデータを平滑化する Tophat2DKernel 幅5画素:
>>> tophat_kernel = Tophat2DKernel(5)
>>> smoothed_data_tophat = convolve(data_2D, tophat_kernel)
原図は以下のとおりである.
以下の図は,シミュレーションデータに適用したいくつかの2 Dコア間の違いを説明する図である.本来の画像と比較してカラーマークがやや異なることに注意されたい。
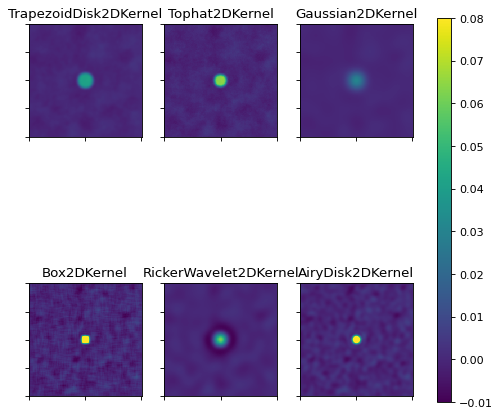
ガウス核は直方体やトップハットよりも滑らかな特性を持つ.直方体フィルタは等方性ではなく,傷が生じる可能性がある(ソースは矩形として表示される).Rickerウェーブレットフィルタは、ノイズおよび緩やかに変化する構造(すなわち、背景)を除去するが、信号源の周囲に負のループが生成される。フィルタの最適な選択はアプリケーションに大きく依存する.
利用可能なカーネル¶
|
2 D Aryディスクカーネル。 |
|
1次元ボックスフィルタカーネル。 |
|
2 D直方体フィルタコア。 |
|
フィルタカーネルは、リストまたは配列から作成されます。 |
|
一次元ガウスフィルタリングコア。 |
|
二次元ガウスフィルタリング核。 |
|
1 D Rickerウェーブレットフィルタリングコア(“メキシコキャップ”コアとも呼ばれることがあります)。 |
|
2 D Rickerウェーブレットフィルタリングカーネル(“メキシコキャップ”カーネルと呼ばれることもあります)。 |
|
1次元モデルからカーネルを作成する. |
|
2 Dモデルからカーネルを作成します。 |
|
2 Dリングフィルタコア。 |
|
2 D TOPHATフィルタコア。 |
|
一次元台形核。 |
|
二次元台形核。 |
核算数.¶
足し算と引き算¶
畳み込みは線形演算であるため、カーネルは互いに加算または減算することができる。それらはまたある数字と掛け合わせることができる。
実例.¶
カーネル削減の基本的な例は、ガウスフィルタの差を定義することである。
>>> from astropy.convolution import Gaussian1DKernel
>>> gauss_1 = Gaussian1DKernel(10)
>>> gauss_2 = Gaussian1DKernel(16)
>>> DoG = gauss_2 - gauss_1
もう1つの応用は,偽造データを機器応答関数モデルと畳み込みすることである.例えば、応答関数が2つのガウスの重み付き和で記述されることができる場合:
>>> gauss_1 = Gaussian1DKernel(10)
>>> gauss_2 = Gaussian1DKernel(16)
>>> SoG = 4 * gauss_1 + gauss_2
多くの場合,生成されたカーネルは,以下の命令を明示的に呼び出すことで標準化する必要がある.
>>> SoG.normalize()
畳み込み.¶
また、2つのカーネルは互いに畳み込むことができ、これは、2つの異なるタイプのカーネルフィルタデータを使用したり、新しい特殊なカーネルを作成する際に非常に有用である。
実例.¶
2つのカーネルを互いに畳むためには、以下の操作を実行してください。
>>> from astropy.convolution import Gaussian1DKernel, convolve
>>> gauss_1 = Gaussian1DKernel(10)
>>> gauss_2 = Gaussian1DKernel(16)
>>> broad_gaussian = convolve(gauss_2, gauss_1)
あるいは多段平滑化の場合:
>>> import numpy as np
>>> from astropy.modeling.models import Lorentz1D
>>> from astropy.convolution import convolve, Gaussian1DKernel, Box1DKernel
>>> lorentz = Lorentz1D(1, 0, 1)
>>> x = np.linspace(-5, 5, 100)
>>> data_1D = lorentz(x) + 0.1 * (np.random.rand(100) - 0.5)
>>> gauss = Gaussian1DKernel(3)
>>> box = Box1DKernel(5)
>>> smoothed_gauss = convolve(data_1D, gauss)
>>> smoothed_gauss_box = convolve(smoothed_gauss, box)
あなたはむしろ以下の操作を実行したいです。
>>> gauss = Gaussian1DKernel(3)
>>> box = Box1DKernel(5)
>>> smoothed_gauss_box = convolve(data_1D, convolve(box, gauss))
これは、通常よりもはるかに大きいデータアレイと1回の畳み込みを行う必要があるので、多くの場合も第1の方法よりも速いであろう。
離散化する.¶
離散畳み込みのカーネルアレイを得るために,カーネルの応答関数をメッシュ上で計算する. discretize_model() それがそうです。離散化ステップには,以下のようなモデルが利用可能である.
型
'center'(デフォルト)グリッド上の応答関数は、バーの中心の値をとることによって計算される。>>> from astropy.convolution import Gaussian1DKernel >>> gauss_center = Gaussian1DKernel(3, mode='center')
型
'linear_interp'ボックス角点の値を取得し、中心における値を線形補間する。>>> gauss_interp = Gaussian1DKernel(3, mode='linear_interp')
型
'oversample'応答関数は,オーバーサンプリンググリッドの平均値をとることで計算される。オーバーサンプリング因子は使用できますfactor論争する。オーバーサンプリング因子が大きすぎると評価が遅くなる。
>>> gauss_oversample = Gaussian1DKernel(3, mode='oversample', factor=10)
型
'integrate'画素上に関数を統合し、使用するscipy.integrate.quadそしてscipy.integrate.dblquadそれがそうです。このパターンは速度が非常に遅く,最も高い精度が必要な場合にのみ使用が推奨されている.
>>> gauss_integrate = Gaussian1DKernel(3, mode='integrate')
特に、カーネル幅が数画素のみの範囲では、このモードを使用することが有利である可能性がある oversample あるいは…。 integrate 積分をサブピクセル尺度に保持する.
正規化する¶
カーネルモデルは、デフォルトで仕様化されています(すなわち、 \(\int_{{-\infty}}^{{\infty}} f(x) dx = 1\) )である。しかし,限られたカーネル配列サイズのため,無限応答を持つカーネルの正規化は1つと異なる可能性がある.この偏差の値はカーネルに格納されている truncation 属性です。
離散化手順によって正規化が異なる可能性があり,特に小さいカーネルに対しては.これは部分的に mode パラメータは,カーネルを初期化する際に行う.(また会いましょう discretize_model() )設ける mode 至る 'oversample' サブピクセル尺度でも規格化を保つことができるようにした.
カーネル配列は呼び出すことで normalize() 方法や方法は normalize_kernel 中のパラメータ convolve() そして convolve_fft() 機能します。後者の方法は,カーネル自体は不変であるが,カーネルの内部標準化バージョンを用いる.
注意してください RickerWavelet1DKernel そして RickerWavelet2DKernel ある \(\int_{{-\infty}}^{{\infty}} f(x) dx = 0\) それがそうです。適切な正規化を定義するために,両フィルタとも正規化されたガウス関数から導出される.